题目内容
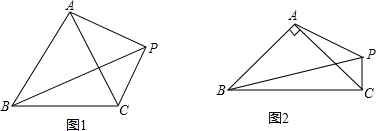
已知:如图1,在△ABC中,AB=AC,∠BAC=α(α不大于90°),点P为△ABC外一点,且∠APC=90°+
α,连接BP
(1)当α=60°时,∠APC= ,PA、PB、PC这三条线段满足的数量关系是 ;
(2)如图2,当α=90°时,探究PA、PB、PC这三条线段满足的数量关系,并证明;
(3)用含α的式子表示PA、PB、PC三条线段满足的数量关系,并证明.
| 1 |
| 2 |
(1)当α=60°时,∠APC=
(2)如图2,当α=90°时,探究PA、PB、PC这三条线段满足的数量关系,并证明;
(3)用含α的式子表示PA、PB、PC三条线段满足的数量关系,并证明.

考点:全等三角形的判定与性质,等腰三角形的性质,等边三角形的性质
专题:
分析:(1)延长AP至点E,使得PE=PC,可得△PCE为等边三角形,即可求证△BCP≌△ACE,可得AE=PB,即可解题;
(2)过C作AP垂线,交AP延长线于点E,易证△BCP∽△ACE,根据对应边比例等于相似比即可求得PB和AE关系,再根据PE和PC关系即可解题;
(3)易证△ABC∽△EPC可得
=
,进而可以证明△BCP∽△ACE,可得
=
=
,根据等腰三角形底边和腰长的计算即可求得PE和PC的关系,即可解题.
(2)过C作AP垂线,交AP延长线于点E,易证△BCP∽△ACE,根据对应边比例等于相似比即可求得PB和AE关系,再根据PE和PC关系即可解题;
(3)易证△ABC∽△EPC可得
| AC |
| CE |
| BC |
| PC |
| PB |
| AE |
| CP |
| CE |
| BC |
| AC |
解答:解:(1)延长AP至点E,使得PE=PC,
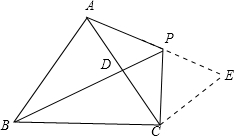
∵∠APC=120°,
∴∠CPE=60°,
∵PE=PC,
∴△PCE为等边三角形,
∴∠PCE=60°,CE=CP,
∵∠PCB=∠ACP+∠ACB,∠ACE=∠PCE+∠ACP,∠ACB=∠PCE=60°,
∴∠BCP=∠ACE,
在△BCP和△ACE中,
,
∴△BCP≌△ACE(SAS),
∴AE=BP,
∵AE=PA+PE,PE=PC,
∴PB=PA+PC;
(2)过C作AP垂线,交AP延长线于点E,
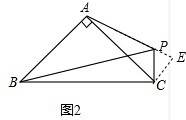
∵∠APC=90°+45°=135°,
∴∠CPE=45°,
∴CE=PE=
PC,
∵∠ACB=∠PCE=45°,
∴∠BCP=∠ACE,
∵
=
,
∴△BCP∽△ACE,
∴
=
,
∴PB=
AE=
(PA+PE)=
(PA+
PC)=
PA+PC;
(3)延长AP至点E,使得∠PCE=90°-
α,

∵AB=AC,∠BAC=α,
∴∠BCA=90°-
α,
∵∠APC=90°+
α,
∴∠CPE=90°-
α,
∴∠PCE=∠CPE=∠ABC=∠ACB,
∴△ABC∽△EPC,∠BCP=∠CE,
∴
=
,即
=
,
∴△BCP∽△ACE,
∴
=
=
,
∵AB=AC,∠BAC=α,
∴BC=2AC•sin
α,
同理PC=2PE•sin
α,∴PE=
,
∴
=
=2•sin
α,
∴PB=2PA•sin
α+PC.

∵∠APC=120°,
∴∠CPE=60°,
∵PE=PC,
∴△PCE为等边三角形,
∴∠PCE=60°,CE=CP,
∵∠PCB=∠ACP+∠ACB,∠ACE=∠PCE+∠ACP,∠ACB=∠PCE=60°,
∴∠BCP=∠ACE,
在△BCP和△ACE中,
|
∴△BCP≌△ACE(SAS),
∴AE=BP,
∵AE=PA+PE,PE=PC,
∴PB=PA+PC;
(2)过C作AP垂线,交AP延长线于点E,

∵∠APC=90°+45°=135°,
∴∠CPE=45°,
∴CE=PE=
| ||
| 2 |
∵∠ACB=∠PCE=45°,
∴∠BCP=∠ACE,
∵
| AC |
| BC |
| ||
| 2 |
∴△BCP∽△ACE,
∴
| BP |
| AE |
| 2 |
∴PB=
| 2 |
| 2 |
| 2 |
| ||
| 2 |
| 2 |
(3)延长AP至点E,使得∠PCE=90°-
| 1 |
| 2 |

∵AB=AC,∠BAC=α,
∴∠BCA=90°-
| 1 |
| 2 |
∵∠APC=90°+
| 1 |
| 2 |
∴∠CPE=90°-
| 1 |
| 2 |
∴∠PCE=∠CPE=∠ABC=∠ACB,
∴△ABC∽△EPC,∠BCP=∠CE,
∴
| AC |
| BC |
| CE |
| PC |
| AC |
| CE |
| BC |
| PC |
∴△BCP∽△ACE,
∴
| PB |
| AE |
| CP |
| CE |
| BC |
| AC |
∵AB=AC,∠BAC=α,
∴BC=2AC•sin
| 1 |
| 2 |
同理PC=2PE•sin
| 1 |
| 2 |
| PC | ||
2•sin
|
∴
| PB | ||||
PA+
|
| BC |
| AC |
| 1 |
| 2 |
∴PB=2PA•sin
| 1 |
| 2 |
点评:本题考查了全等三角形的判定和全等三角形对应边相等的性质,考查了相似三角形的判定和相似三角形对应边比例相等的性质,本题中求证△BCP与△ACE的全等或相似是解题的关键.

练习册系列答案
 桃李文化快乐暑假武汉出版社系列答案
桃李文化快乐暑假武汉出版社系列答案 优秀生快乐假期每一天全新寒假作业本系列答案
优秀生快乐假期每一天全新寒假作业本系列答案 暑假接力赛新疆青少年出版社系列答案
暑假接力赛新疆青少年出版社系列答案
相关题目
若k为整数,则使方程(k-3)x=2013-4x的解也是整数的k的值有( ) 个.
| A、16 | B、12 | C、9 | D、8 |
 如图,在四边形形ABCD中,∠ADB=∠DBC=90°,AD=6,sinA=
如图,在四边形形ABCD中,∠ADB=∠DBC=90°,AD=6,sinA=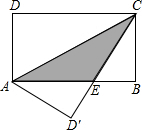 如图,在矩形ABCD中,AB=8,BC=4,将矩形沿AC折叠,CD落在AB上的点为E点,则重叠部分△AEC的面积是多少?
如图,在矩形ABCD中,AB=8,BC=4,将矩形沿AC折叠,CD落在AB上的点为E点,则重叠部分△AEC的面积是多少? 已知,如图,AB=CD,AE=CF,BE=DF,求证:AF∥CE.
已知,如图,AB=CD,AE=CF,BE=DF,求证:AF∥CE. 如图,AC=CD=DB,CM=DM,写出图中哪一个点是哪一条线段的中点.
如图,AC=CD=DB,CM=DM,写出图中哪一个点是哪一条线段的中点. 如图,直线AB、CD交于点O,且∠EOD=65°,∠COF=130°,OB平分∠DOF,问EO与直线AB的位置关系如何?请说明理由.
如图,直线AB、CD交于点O,且∠EOD=65°,∠COF=130°,OB平分∠DOF,问EO与直线AB的位置关系如何?请说明理由.