题目内容
17.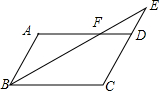 如图,平行四边形ABCD中,E是CD的延长线上一点,BE与AD交于点F,若ED:DC=2:3,△DEF的面积为8,则平行四边形ABCD的面积为60.
如图,平行四边形ABCD中,E是CD的延长线上一点,BE与AD交于点F,若ED:DC=2:3,△DEF的面积为8,则平行四边形ABCD的面积为60.
分析 根据平行四边形的性质得出AB=DC,AD∥BC,AB∥CD,证出△DEF∽△CEB,△DEF∽△ABF,求出△CEB的面积为50,△ABF的面积为18,即可求出答案.
解答 解:∵四边形ABCD是平行四边形,
∴AB=DC,AD∥BC,AB∥CD,
∵ED:DC=2:3,
∴ED:CE=2:5,ED:AB=2:3,
∵AD∥BC,AB∥CD,
∴△DEF∽△CEB,△DEF∽△ABF,
∴$\frac{{S}_{△DEF}}{{S}_{△CEB}}$=($\frac{DE}{CE}$)2=($\frac{2}{5}$)2=$\frac{4}{25}$,$\frac{{S}_{△DEF}}{{S}_{△ABF}}$=($\frac{DE}{AB}$)2=($\frac{2}{3}$)2=$\frac{4}{9}$
∵△DEF的面积为8,
∴△CEB的面积为50,△ABF的面积为18,
∴四边形DFBC的面积为50-8=42,
∴平行四边形ABCD的面积为42+18=60,
故答案为:60.
点评 本题考查了平行四边形的性质,相似三角形的性质和判定的应用,能求出△CEB和△ABF的面积是解此题的关键.

练习册系列答案
相关题目
5.下列有理式中是分式的是( )
| A. | $\frac{1}{5}(x+y)$ | B. | $\frac{a}{3}$ | C. | $\frac{ab}{2}+\frac{1}{c}$ | D. | $\frac{x}{2}+y$ |
7.若m>n,下列不等式不一定成立的是( )
| A. | m+2>n+2 | B. | 2m>2n | C. | -2m<-2n | D. | m2>n2 |
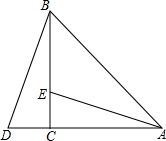 如图,在△ABC中,∠ACB=90°,AC=BC,延长AC到点D,使CD=CE.求证:
如图,在△ABC中,∠ACB=90°,AC=BC,延长AC到点D,使CD=CE.求证: