题目内容
(本题满分12分)
(1)若二次函数y1=mx2 -3(m-1)x+2m-3的图象关于y轴对称;
①求二次函数y1的解析式;
②已知一次函数y2=2x-2,证明:在实数范围内,对于x的同一个值,这两个函数所对应的函数值y1≥y2均成立;
(2)在(1)条件下,若二次函数y3=ax2+bx+c的图象经过点(-5,0),且在实数范围内,对于x的同一个值,这三个函数所对应的函数值y1≥y3≥y2均成立,求二次函数y3=ax2+bx+c的解析式.
(1)①二次函数的解析式为:y1=x2-1;
②证明见解析;
(2)y3= .
.
【解析】
试题分析:(1)①由已知可得3(m-1)=0,得m=1,从而得到二次函数的解析式为:y1=x2-1;
②通过y1-y2=x2-1-(2x-2)=(x-1)2≥0得到证明;
(2)由②知,当x=1时,y1=y2=0,即y1、y2的图象都经过点(1,0);从而知y3的图象必经过(1,0),再由已知y3的图象还过点(-5,0),由待定系数法可求得y3的解析式,再通过计算y3-y2即可.
试题解析:(1)①∵二次函数y1=mx2 -3(m-1)x+2m-3的图象关于y轴对称,∴3(m-1)=0,即m=1,
∴抛物线的解析式为:y1=x2-1;
②∵y1-y2=x2-1-(2x-2)=(x-1)2≥0,∴y1≥y2(当且仅当x=1时,等号成立);
(2)由②知,当x=1时,y1=y2=0,即y1、y2的图象都经过点(1,0);
∵对应x的同一个值,y1≥y3≥y2成立,
∴y3=ax2+bx+c的图象必经过(1,0),
又∵y3=ax2+bx+c经过(-5,0),
∴y3=a(x-1)(x+5)=ax2+4ax-5a;
设y=y3-y2=ax2+4ax-5a-(2x-2)=ax2+(4a-2)x+(2-5a);
对于x的同一个值,这三个函数对应的函数值y1≥y3≥y2成立,
∴y3-y2≥0,
∴y=ax2+(4a-2)x+(2-5a)≥0;
根据y1、y2的图象知:a>0,
∴(4a-2)2-4a(2-5a)≤0,即(3a-1)2≤0,
故a= ,所以y3=
,所以y3= .
.
考点:二次函数的综合题.

 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案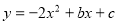 的图像经过点A(0,4)和B(1,-2).
的图像经过点A(0,4)和B(1,-2). 的长为( )
的长为( )

 处开出一高球,球从离地面1米的
处开出一高球,球从离地面1米的 处飞出
处飞出 在
在 轴上),运动员孙可在距
轴上),运动员孙可在距 点6米的
点6米的 处发现球在自己头的正上方达到最高点
处发现球在自己头的正上方达到最高点 ,距地面约4米
,距地面约4米
 距守门员多少米?(取
距守门员多少米?(取 )
) ,他应从第一次落地点
,他应从第一次落地点 )
)