题目内容
16.有5张正面分别标有数字-2,0,2,4,6的不透明卡片,它们除数不同外其余全部相同,先将它们背面朝上,洗匀后从中任取一张,将该卡片上的数字记为a,则使关于x不等式组$\left\{\begin{array}{l}{x>3x-4}\\{3x-a>5}\end{array}\right.$有实数解的概率为$\frac{2}{5}$.分析 分别解两个不等式得到x<2和x>$\frac{5+a}{3}$,若不等式组有实数解,则2>$\frac{5+a}{3}$,解得a<1,然后根据概率公式求解.
解答 解:$\left\{\begin{array}{l}{x>3x-4①}\\{3x-a>5②}\end{array}\right.$,
解①得x<2,
解②得x>$\frac{5+a}{3}$,
不等式组有实数解,则2>$\frac{5+a}{3}$,解得a<1,
所以任取一张,将该卡片上的数字记为a,则使关于x不等式组$\left\{\begin{array}{l}{x>3x-4}\\{3x-a>5}\end{array}\right.$有实数解的概率=$\frac{2}{5}$.
故答案为$\frac{2}{5}$.
点评 本题考查了概率公式:随机事件A的概率P(A)=事件A可能出现的结果数除以所有可能出现的结果数.也考查了解一元一次不等式组.

练习册系列答案
相关题目
6.在数-3,2,-4中任取两个数相乘,其中积最小的是( )
| A. | -6 | B. | -12 | C. | -8 | D. | 12 |
7.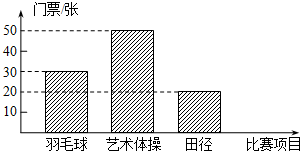 2010年5月20日上午10时起.2010年广州亚运会门票全面发售.下表为抄录广州亚运会官方网公布的三类比赛的部分价格,如图为某公司购买的门票种类、数量所绘制的条形统计图.
2010年5月20日上午10时起.2010年广州亚运会门票全面发售.下表为抄录广州亚运会官方网公布的三类比赛的部分价格,如图为某公司购买的门票种类、数量所绘制的条形统计图.
依据上面的表和图,回答下列问题:
(1)其中观看羽毛球比赛的门票有张;观看田径比赛的门票占全部门票的;
(2)公司决定采用随机抽取的方式把门票分别配给部分员工,在看不到门票的条件下,每人抽取一张(假设所有的门票形状、大小、质地等完全相同且充分洗匀),问员工小丽抽到艺术体操门票的概率是$\frac{1}{2}$;
(3)若该公司购买全部门票共花36000元,试求每张田径门票的价格.
 2010年5月20日上午10时起.2010年广州亚运会门票全面发售.下表为抄录广州亚运会官方网公布的三类比赛的部分价格,如图为某公司购买的门票种类、数量所绘制的条形统计图.
2010年5月20日上午10时起.2010年广州亚运会门票全面发售.下表为抄录广州亚运会官方网公布的三类比赛的部分价格,如图为某公司购买的门票种类、数量所绘制的条形统计图.| 比赛项目 | 票价(元/张) |
| 羽毛球 | 400 |
| 艺术体操 | 240 |
| 田径 | x |
(1)其中观看羽毛球比赛的门票有张;观看田径比赛的门票占全部门票的;
(2)公司决定采用随机抽取的方式把门票分别配给部分员工,在看不到门票的条件下,每人抽取一张(假设所有的门票形状、大小、质地等完全相同且充分洗匀),问员工小丽抽到艺术体操门票的概率是$\frac{1}{2}$;
(3)若该公司购买全部门票共花36000元,试求每张田径门票的价格.
4.能够使二次根式$\sqrt{2x-3}$有意义的实数x的取值范围是( )
| A. | x$>\frac{3}{2}$ | B. | x$≥\frac{3}{2}$ | C. | x$<\frac{3}{2}$ | D. | x$≤\frac{2}{3}$ |
11.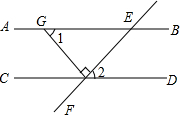 如图,AB∥CD,EF交AB、CD于点E、F,FG⊥EF交AB于点G,若∠1=50°,则∠2的度数是( )
如图,AB∥CD,EF交AB、CD于点E、F,FG⊥EF交AB于点G,若∠1=50°,则∠2的度数是( )
 如图,AB∥CD,EF交AB、CD于点E、F,FG⊥EF交AB于点G,若∠1=50°,则∠2的度数是( )
如图,AB∥CD,EF交AB、CD于点E、F,FG⊥EF交AB于点G,若∠1=50°,则∠2的度数是( )| A. | 40° | B. | 50° | C. | 70° | D. | 140° |