题目内容
17.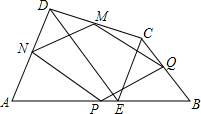 如图,点E为AB上一点,以AE,BE为边在AB同侧作等边△AED和等边△BEC,点P,Q,M,N分别是AB,BC,CD,DA的中点.
如图,点E为AB上一点,以AE,BE为边在AB同侧作等边△AED和等边△BEC,点P,Q,M,N分别是AB,BC,CD,DA的中点.(1)判断四边形PNMQ的形状,并证明;
(2)∠NPQ的度数为120°(直接写出结果).
分析 (1)易证△AEC≌△DEB得AC=DB,根据AB、BC、CD、DA的中点分别为P、Q、M、N,可证PQ=MN=$\frac{1}{2}$AC,PQ∥MN∥AC,四边形PQMN为平行四边形,根据邻边相等的平行四边形可以判定为菱形;
(2)利用(1)中全等三角形的对应角相等得到:∠ACE=∠DBE.结合等边三角形的性质和三角形外角定理推知∠CAE+∠DBE=60°,由三角形内角和定理求得
∠NPQ=∠AOB=120°.
解答 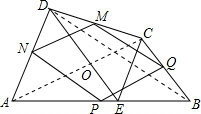 解:(1)四边形PNMQ为菱形.证明如下:
解:(1)四边形PNMQ为菱形.证明如下:
连接AC、BD,且AC、BD交于点O.
在△AEC与△DEB中,
$\left\{\begin{array}{l}{AE=DE}\\{∠AEC=∠DEB}\\{CE=BE}\end{array}\right.$,
∴△AEC≌△DEB(SAS),
∴AC=DB,
∵AB、BC、CD、DA的中点分别为P、Q、M、N,
∴PQ=MN=$\frac{1}{2}$AC,PQ∥MN∥AC,
∴四边形PNMQ为平行四边形,
同理MQ=$\frac{1}{2}$BD,
∴MQ=PQ,
∴四边形PNMQ为菱形;
(2)由(1)知,△AEC≌△DEB,则∠ACE=∠DBE.
∵∠CAE+∠ACE=60°,∠CAE+∠DBE=60°,
∴∠AOB=180°-60°=120°,
∴∠NPQ=∠AOB=120°.
故答案是:120°.
点评 本题考查了中点四边形,菱形的判定,全等三角形的判定与性质的运用,解答时证明三角形全等是关键.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
2.已知一次函数y=(m-3)x+m-4的图象不经过第二象限,则m的取值范围是( )
| A. | m>3 | B. | m>4 | C. | 3<m<4 | D. | 3<m≤4 |
9.下列命题错误的有( )
①实数与数轴上的点一一对应;
②无限小数就是无理数;
③直线外一点到这条直线的垂线段叫做点到直线的距离;
④两条直线被第三条直线所截,同旁内角互补.
①实数与数轴上的点一一对应;
②无限小数就是无理数;
③直线外一点到这条直线的垂线段叫做点到直线的距离;
④两条直线被第三条直线所截,同旁内角互补.
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
7.已知a-b=3,ab=2,则a2+b2的值是( )
| A. | 3 | B. | 13 | C. | 9 | D. | 11 |
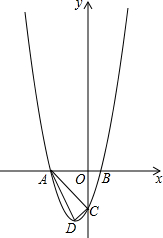 如图,抛物线y=x2+bx+c的顶点为D(-1,-4),与y轴交于点C(0,-3),与x轴交于A,B两点(点A在点B的左侧).
如图,抛物线y=x2+bx+c的顶点为D(-1,-4),与y轴交于点C(0,-3),与x轴交于A,B两点(点A在点B的左侧).