题目内容
6.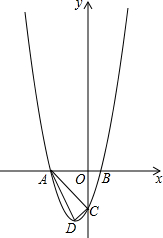 如图,抛物线y=x2+bx+c的顶点为D(-1,-4),与y轴交于点C(0,-3),与x轴交于A,B两点(点A在点B的左侧).
如图,抛物线y=x2+bx+c的顶点为D(-1,-4),与y轴交于点C(0,-3),与x轴交于A,B两点(点A在点B的左侧).(1)求抛物线的解析式;
(2)连接AC,CD,AD,试证明△ACD为直角三角形.
分析 (1)由于已知抛物线顶点坐标,则可设顶点式y=a(x+1)2-4,然后把(0,-3)代入求出a即可;
(2)先根据抛物线与x轴的交点问题确定A点坐标,再利用两点间的距离公式分别计算出AC、CD、AD,然后根据勾股定理的逆定理判断△ACD为直角三角形.
解答 (1)解:设抛物线解析式为y=a(x+1)2-4,
把(0,-3)代入得a-4=-3,解得a=1,
所以抛物线解析式为y=(x+1)2-4;
(2)证明:当y=0时,(x+1)2-4=0,解得x1=-3,x2=1,则A(-3,0),B(1,0),
因为AC2=32+32=18,AD2=(-1+3)2+(-4)2=20,DC2=(-1)2+(-4+3)2=2,
所以AC2+DC2=AD2,
所以△ACD为直角三角形.
点评 本题考查了待定系数法求二次函数的解析式:在利用待定系数法求二次函数关系式时,要根据题目给定的条件,选择恰当的方法设出关系式,从而代入数值求解.一般地,当已知抛物线上三点时,常选择一般式,用待定系数法列三元一次方程组来求解;当已知抛物线的顶点或对称轴时,常设其解析式为顶点式来求解;当已知抛物线与x轴有两个交点时,可选择设其解析式为交点式来求解.也考查了两点间的距离公式和勾股定理的逆定理.

练习册系列答案
 轻松夺冠全能掌控卷系列答案
轻松夺冠全能掌控卷系列答案
相关题目
11.一件商品的标价为120元,为了促销打七折售出后可获利5%.则此商品的进价为( )
| A. | 80元 | B. | 85元 | C. | 90元 | D. | 95元 |
16.下列式子是一元一次不等式的是( )
| A. | x+y≤0 | B. | x2≥0 | C. | $\frac{x}{2}$>3+x | D. | $\frac{1}{x}$<0 |
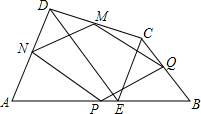 如图,点E为AB上一点,以AE,BE为边在AB同侧作等边△AED和等边△BEC,点P,Q,M,N分别是AB,BC,CD,DA的中点.
如图,点E为AB上一点,以AE,BE为边在AB同侧作等边△AED和等边△BEC,点P,Q,M,N分别是AB,BC,CD,DA的中点.