题目内容
8.(1)计算:($2\sqrt{24}$-$\sqrt{18}$)÷$\sqrt{3}$+$2\sqrt{\frac{3}{2}}$;(2)解方程:x2-2x-3=0;
(3)解方程:2x2+5x-3=0.
分析 (1)先根据二次根式的除法法则运算,然后把各二次根式化为最简二次根式后合并即可;
(2)利用因式分解法解方程;
(3)利用因式分解法解方程.
解答 解:(1)原式=2$\sqrt{24÷3}$-$\sqrt{18÷3}$+$\sqrt{6}$
=4$\sqrt{2}$-$\sqrt{6}$+$\sqrt{6}$
=4$\sqrt{2}$;
(2)(x-3)(x+1)=0,
x-3=0或x+1=0,
所以x1=3,x2=-1;
(3)(2x-1)(x+3)=0,
2x-1=0或x+3=0,
所以x1=$\frac{1}{2}$,x2=-3.
点评 本题考查了二次根式的计算:先把各二次根式化为最简二次根式,再进行二次根式的乘除运算,然后合并同类二次根式.也考查了因式分解法解一元二次方程.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
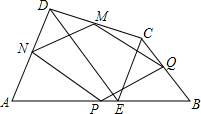 如图,点E为AB上一点,以AE,BE为边在AB同侧作等边△AED和等边△BEC,点P,Q,M,N分别是AB,BC,CD,DA的中点.
如图,点E为AB上一点,以AE,BE为边在AB同侧作等边△AED和等边△BEC,点P,Q,M,N分别是AB,BC,CD,DA的中点.