题目内容
1.已知:在△ABC中,AC=BC,∠ACB=90°,点D是AB的中点,点E是AB边上一点.(1)直线BF垂直于直线CE,交CE于点F,交CD于点G(如图①),求证:AE=CG;
(2)直线AH垂直于直线CE,交CE的延长线于点H,交CD的延长线于点M(如图②),找出图中与BE相等的线段,并证明.

分析 (1)首先根据点D是AB中点,∠ACB=90°,可得出∠ACD=∠BCD=45°,判断出△AEC≌△CGB,即可得出AE=CG;
(2)根据垂直的定义得出∠CMA+∠MCH=90°,∠BEC+∠MCH=90°,再根据AC=BC,∠ACM=∠CBE=45°,得出△BCE≌△CAM,进而证明出BE=CM.
解答 (1)证明:
∵点D是AB中点,AC=BC,∠ACB=90°,
∴CD⊥AB,∠ACD=∠BCD=45°,
∴∠CAD=∠CBD=45°,
∴∠CAE=∠BCG,
又∵BF⊥CE,
∴∠CBG+∠BCF=90°,
又∵∠ACE+∠BCF=90°,
∴∠ACE=∠CBG,
在△AEC和△CGB中,
$\left\{\begin{array}{l}{∠CAE=∠BCG}\\{AC=BC}\\{∠ACE=∠CBG}\end{array}\right.$
∴△AEC≌△CGB(ASA),
∴AE=CG;
(2)解:BE=CM.
证明:∵CH⊥HM,CD⊥ED,
∴∠CMA+∠MCH=90°,∠BEC+∠MCH=90°,
∴∠CMA=∠BEC,
又∵∠ACM=∠CBE=45°,
在△BCE和△CAM中,
$\left\{\begin{array}{l}{∠BEC=∠CMA}\\{∠CBE=∠ACM}\\{BC=AC}\end{array}\right.$,
∴△BCE≌△CAM(AAS),
∴BE=CM.
点评 本题主要考查全等三角形的判定和性质,掌握全等三角形的判定方法(即SSS、SAS、ASA、AAS和HL)和全等三角形的性质(即对应边相等、对应角相等)是解题的关键.

练习册系列答案
相关题目
6. 如图所示,$\frac{AD}{AE}$=$\frac{AC}{AB}$=$\frac{1}{3}$,则下列结论不成立的是( )
如图所示,$\frac{AD}{AE}$=$\frac{AC}{AB}$=$\frac{1}{3}$,则下列结论不成立的是( )
 如图所示,$\frac{AD}{AE}$=$\frac{AC}{AB}$=$\frac{1}{3}$,则下列结论不成立的是( )
如图所示,$\frac{AD}{AE}$=$\frac{AC}{AB}$=$\frac{1}{3}$,则下列结论不成立的是( )| A. | △ABE∽△ACD | B. | △BOD∽△COE | C. | OC=OD | D. | CD:BE=1:3 |
11.下列运算正确的是( )
| A. | 3a+2b=5ab | B. | -2(a-1)=-2a+1 | C. | -5x2+3x2=-2x2 | D. | a3-a2=a |
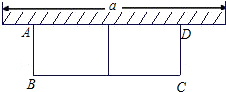 如图,要利用一面墙(墙的最大可用长度a为13m)建羊圈,用24米的围栏围成两个大小相同的矩形羊圈,设羊圈的宽AB为x(m),总面积为S(m2).
如图,要利用一面墙(墙的最大可用长度a为13m)建羊圈,用24米的围栏围成两个大小相同的矩形羊圈,设羊圈的宽AB为x(m),总面积为S(m2). 如图,在⊙O中,∠AOB=62°,则∠ACB=31度.
如图,在⊙O中,∠AOB=62°,则∠ACB=31度. 如图,在6×8的网格图中,每个小正方形边长均为1,原点O和△ABC的顶点均为格点.
如图,在6×8的网格图中,每个小正方形边长均为1,原点O和△ABC的顶点均为格点.