题目内容
2. 如图,在梯形ABCD中,AD∥BC,AB⊥BC,若AD=2,tan∠ACB=$\frac{3}{4}$,梯形ABCD的面积是9.
如图,在梯形ABCD中,AD∥BC,AB⊥BC,若AD=2,tan∠ACB=$\frac{3}{4}$,梯形ABCD的面积是9.(1)求AB的长;
(2)求tan∠ABD的值.
分析 (1)根据题意设AB=3x,BC=4x,根据梯形面积公式列出关于x的方程,求出x的值,得到AB的长;
(2)根据正切的定义求出tan∠ABD的值.
解答 解:(1)设AB=3x,则BC=4x,
由题意得,$\frac{1}{2}$×(2+4x)×3x=9,
整理得,2x2+x-3=0,
解得,x1=1,x2=-$\frac{3}{2}$(舍去),
∴AB=3;
(2)在Rt△ABD中,AD=2,AB=3,
∴tan∠ABD=$\frac{AD}{AB}$=$\frac{2}{3}$.
点评 本题考查的是梯形的性质、一元二次方程的解法和锐角三角函数的知识,掌握锐角三角函数的概念是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
14.将点A(3,-1)先向左平移3个单位,再向上平移2个单位,那么点A的对应点A′的坐标是( )
| A. | (6,1) | B. | (0,-3) | C. | (0,1) | D. | (6,-3) |
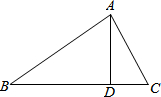 如图,点D在线段BC上,已知∠BAC=90°,∠DAC+∠C=90°,则∠BAD和∠C的大小关系是∠BAD=∠C,其依据是同角的余角相等.
如图,点D在线段BC上,已知∠BAC=90°,∠DAC+∠C=90°,则∠BAD和∠C的大小关系是∠BAD=∠C,其依据是同角的余角相等.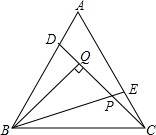 如图,点D,E分别是等边△ABC的两边AB,AC上的点,且AD=CE,BQ⊥CD于点Q,PQ=1,求BQ的长.
如图,点D,E分别是等边△ABC的两边AB,AC上的点,且AD=CE,BQ⊥CD于点Q,PQ=1,求BQ的长.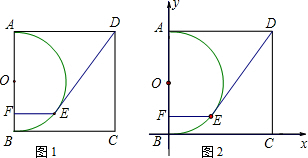
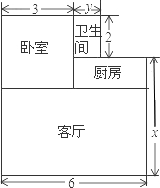 老李购买了一套学位房,他准备将地面铺上地砖,地面结构如图所示.
老李购买了一套学位房,他准备将地面铺上地砖,地面结构如图所示. 请采用两种不同的方法,在如图的方格纸中画出两条互相垂直的直线.
请采用两种不同的方法,在如图的方格纸中画出两条互相垂直的直线.