题目内容
17.已知⊙O的半径为R,点O到直线m的距离为d,R、d是方程x2-4x+a=0的两根,当直线m与⊙O相切时,a=4.分析 若直线和圆相切,则d=r.即方程有两个相等的实数根,得16-4a=0,a=4.
解答 解:∵直线和圆相切,
∴d=r,
∴△=16-4a=0,
∴a=4,
故答案为:4
点评 此题考查了直线和圆的位置关系与数量关系之间的联系,关键是熟练运用根的判别式判断方程的根的情况.

练习册系列答案
相关题目
7.已知∠α的补角为125°12′,则它的余角为( )
| A. | 35°12′ | B. | 35°48′ | C. | 55°12′ | D. | 55°48′ |
9.在下列函数中表示关于x的反比例函数的是( )
| A. | y=2x | B. | y=$\frac{2}{x}$ | C. | y=$\frac{2}{x+1}$ | D. | y=$\frac{2}{{x}^{2}}$ |
7.若点P(x,y)在第一象限,则点Q(x+y,x-y)一定不在( )
| A. | 第一、二象限 | B. | 第三、四象限 | C. | 第二、三象限 | D. | 第二、四象限 |
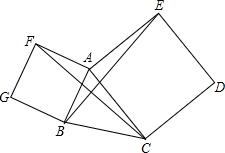 已知,如图,分别以△ABC的边AC,AB为边的三角形作正方形ACDE、BAFG.
已知,如图,分别以△ABC的边AC,AB为边的三角形作正方形ACDE、BAFG.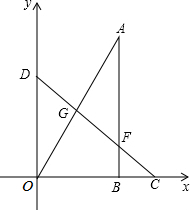 如图,将两块直角三角板摆放在平面直角坐标系中,有∠COD=∠ABO=Rt∠,∠OCD=45°,∠AOB=60°,且AO=CD=8.现将Rt△AOB绕点O逆时针旋转,旋转角为β(0°≤β≤180°).在旋转过程中,直线CD分别与直线AB,OA交于点F,G.
如图,将两块直角三角板摆放在平面直角坐标系中,有∠COD=∠ABO=Rt∠,∠OCD=45°,∠AOB=60°,且AO=CD=8.现将Rt△AOB绕点O逆时针旋转,旋转角为β(0°≤β≤180°).在旋转过程中,直线CD分别与直线AB,OA交于点F,G. 如图,在梯形ABCD中,AD∥BC,AB⊥BC,若AD=2,tan∠ACB=$\frac{3}{4}$,梯形ABCD的面积是9.
如图,在梯形ABCD中,AD∥BC,AB⊥BC,若AD=2,tan∠ACB=$\frac{3}{4}$,梯形ABCD的面积是9.