题目内容
解下列方程
(1)(2x-1)2=9;
(2)-3x2-4x+4=0;
(3)x2-2x-3=0;
(4)(x-3)2+4x(x-3)=0.
(1)(2x-1)2=9;
(2)-3x2-4x+4=0;
(3)x2-2x-3=0;
(4)(x-3)2+4x(x-3)=0.
考点:解一元二次方程-因式分解法
专题:
分析:(1)开方后即可得出两个一元一次方程,求出方程的解即可;
(2)先分解因式,即可得出两个一元一次方程,求出方程的解即可;
(3)先分解因式,即可得出两个一元一次方程,求出方程的解即可;
(4)先分解因式,即可得出两个一元一次方程,求出方程的解即可.
(2)先分解因式,即可得出两个一元一次方程,求出方程的解即可;
(3)先分解因式,即可得出两个一元一次方程,求出方程的解即可;
(4)先分解因式,即可得出两个一元一次方程,求出方程的解即可.
解答:解:(1)两边开方得:2x-1=±3,
解得:x1=2,x2=-1;
(2)-3x2-4x+4=0,
(-3x-2)(x+2)=0,
-3x-2=0,x+2=0,
x1=
,x2=-2;
(3)x2-2x-3=0,
(x-3)(x+1)=0,
x-3=0,x+1=0,
x1=3,x2=-1;
(4)分解因式得:(x-3)(x-3+4x)=0,
x-3=0,x-3+4x=0,
x1=3,x2=
.
解得:x1=2,x2=-1;
(2)-3x2-4x+4=0,
(-3x-2)(x+2)=0,
-3x-2=0,x+2=0,
x1=
| 2 |
| 3 |
(3)x2-2x-3=0,
(x-3)(x+1)=0,
x-3=0,x+1=0,
x1=3,x2=-1;
(4)分解因式得:(x-3)(x-3+4x)=0,
x-3=0,x-3+4x=0,
x1=3,x2=
| 3 |
| 5 |
点评:本题考查了解一元二次方程的应用,解此题的关键是能把一元二次方程转化成一元一次方程,难度适中.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
在平面直角坐标系中,位于第四象限的点是( )
| A、(1,-2) |
| B、(2,1) |
| C、(-2,1) |
| D、(-1,-3) |
在下列图形的特征中,平行四边形不一定具有的是( )
| A、对角相等 |
| B、对角互补 |
| C、邻角互补 |
| D、内角和是180度 |
一个数的平方根和立方根都等于它本身,则这个数是( )
| A、0 | B、0、±1 | C、0、1 | D、1 |
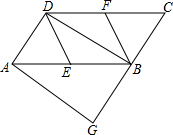 如图,在?ABCD中,∠DAB=60°,AB=2AD,点E是AB的中点,过点A作AG∥BD,交CB的延长线于点G.请判断四边形AGBD是什么特殊四边形?并加以证明.
如图,在?ABCD中,∠DAB=60°,AB=2AD,点E是AB的中点,过点A作AG∥BD,交CB的延长线于点G.请判断四边形AGBD是什么特殊四边形?并加以证明.