题目内容
1. 已知如图,点O为?ABCD对角线BD的中点,EF过点O与AD、BC分别相交于点E、F.
已知如图,点O为?ABCD对角线BD的中点,EF过点O与AD、BC分别相交于点E、F.(1)求证:△EOD≌△FOB;
(2)若B、D两点关于EF对称,连结BE、DF,请判断四边形EBFD为何种四边形?并说明理由.
分析 (1)利用平行四边形的性质以及全等三角形的判定方法ASA得出△DOE≌△BOF即可;
(2)首先利用一组对边平行且相等的四边形是平行四边形得出四边形EBFD是平行四边形,由对称的性质得出EF⊥BD,即可得出结论.
解答 (1)证明:∵在?ABCD中,O为对角线BD的中点,
∴BO=DO,AD∥BC,
∴∠EDB=∠FBO,
在△EOD和△FOB中,$\left\{\begin{array}{l}{∠EDO=∠OBF}&{\;}\\{DO=BO}&{\;}\\{∠EOD=∠FOB}&{\;}\end{array}\right.$,
∴△DOE≌△BOF(ASA);
(2)解: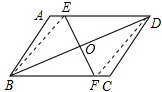 四边形EBFD为菱形,理由如下:如图所示:
四边形EBFD为菱形,理由如下:如图所示:
∵△DOE≌△BOF,
∴OE=OF,
又∵OB=OD
∴四边形EBFD是平行四边形,
∵B、D两点关于EF对称,
∴EF⊥BD,
∴四边形EBFD为菱形.
点评 此题主要考查了平行四边形的性质与判定、全等三角形的判定与性质、菱形的判定等知识;熟练掌握平行四边形的判定与性质,证明三角形全等是解决问题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
12.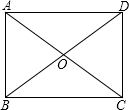 如图,在矩形ABCD中,下列结论不正确的是( )
如图,在矩形ABCD中,下列结论不正确的是( )
 如图,在矩形ABCD中,下列结论不正确的是( )
如图,在矩形ABCD中,下列结论不正确的是( )| A. | △AOB的等腰三角形 | |
| B. | S△ABO=S△ADO | |
| C. | AC⊥BD | |
| D. | 当∠ABD=45°时,矩形ABCD会变成正方形 |
6.满足下列条件的三条线段a、b、c能构成三角形的是( )
| A. | a:b:c=1:2:3 | B. | a+b=4,a+b+c=9 | C. | a=3,b=4,c=5 | D. | a:b:c=1:1:2 |
10.若一个正多边形的一个外角是36°,则这个正多边形的边数是( )
| A. | 1 0 | B. | 9 | C. | 8 | D. | 6 |
 如图,在矩形ABCD中,AB<BC,M是BC的中点,DE⊥AM于点E,且AB、BC的长是一元二次方程x2-7x+12=0的两根,求△DEM的面积.
如图,在矩形ABCD中,AB<BC,M是BC的中点,DE⊥AM于点E,且AB、BC的长是一元二次方程x2-7x+12=0的两根,求△DEM的面积. 已知:如图,△ABC中,DE∥BC,EF∥AB,BE平分∠ABC.
已知:如图,△ABC中,DE∥BC,EF∥AB,BE平分∠ABC. 在平面直角坐标系xOy中,过象限内一点分别作坐标轴的垂线,若与坐标轴围成的矩形的周长与面积相等,则这个点叫做“和谐点”.如图,过点H(-3,6)分别作x轴,y轴的垂线,与坐标轴围成的矩形OAHB的周长与面积相等,则点H(3,6)是“和谐点”.
在平面直角坐标系xOy中,过象限内一点分别作坐标轴的垂线,若与坐标轴围成的矩形的周长与面积相等,则这个点叫做“和谐点”.如图,过点H(-3,6)分别作x轴,y轴的垂线,与坐标轴围成的矩形OAHB的周长与面积相等,则点H(3,6)是“和谐点”.