题目内容
 在直角坐标系xOy中,?ABCD四个顶点的坐标分别为A(1,1),B(4,1),C(5,2),D(2,2),直线l:y=kx+b与直线y=-2x平行.
在直角坐标系xOy中,?ABCD四个顶点的坐标分别为A(1,1),B(4,1),C(5,2),D(2,2),直线l:y=kx+b与直线y=-2x平行.(1)k=
(2)若直线l过点D,求直线l的解析式;
(3)若直线l同时与边AB和CD都相交,求b的取值范围;
(4)若直线l沿线段AC从点A平移至点C,设直线l与x轴的交点为P,问是否存在一点P,使△PAB为等腰三角形?若存在,直接写出点P的坐标;若不存在,请说明理由.
考点:一次函数综合题
专题:
分析:(1)根据平行的条件,一次项系数相同,据此即可求得;
(2)设直线l的解析式是y=-2x+b,把D的坐标代入解析式即可求得b的值,即可得到函数的解析式;
(3)求得经过A和C的解析式,即可求得;
(4)分成PA=PB和AP=AB和BP=BA三种情况进行讨论即可求解.
(2)设直线l的解析式是y=-2x+b,把D的坐标代入解析式即可求得b的值,即可得到函数的解析式;
(3)求得经过A和C的解析式,即可求得;
(4)分成PA=PB和AP=AB和BP=BA三种情况进行讨论即可求解.
解答:解:(1)k=-2;
(2)设直线l的解析式是y=-2x+b,
把(2,2)代入得:-4+b=2,解得:b=6,
则直线l的解析式是y=-2x+6;
(3)设过A直线l的解析式是y=-2x+b,把(1,1)代入得:-2+c=1,解得:c=3,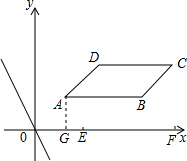
则直线的解析式是y=-2x+3,
同理,过C直线l的解析式是y=-2x+12,
则3≤b≤12;
(4)当直线l经过A时,解析式是y=-2x+3,令y=0,解得x=
,即与x轴的交点是E(
,0);
当直线l经过C时,解析式是y=-2x+12,令y=0,解得x=6,即与x轴的交点是F(6,0);
当PA=PB时,P在AB的中垂线上,则P的坐标是(
,0);
当AP=AB=3时,则PG=
=2
,则P的坐标是(2
+1,0);
同理,当BP=BA=3时,P的坐标是(4-2
,0).
故P的坐标是:(
,0)或(2
+1,0)或(4-2
,0).
(2)设直线l的解析式是y=-2x+b,
把(2,2)代入得:-4+b=2,解得:b=6,
则直线l的解析式是y=-2x+6;
(3)设过A直线l的解析式是y=-2x+b,把(1,1)代入得:-2+c=1,解得:c=3,

则直线的解析式是y=-2x+3,
同理,过C直线l的解析式是y=-2x+12,
则3≤b≤12;
(4)当直线l经过A时,解析式是y=-2x+3,令y=0,解得x=
| 3 |
| 2 |
| 3 |
| 2 |
当直线l经过C时,解析式是y=-2x+12,令y=0,解得x=6,即与x轴的交点是F(6,0);
当PA=PB时,P在AB的中垂线上,则P的坐标是(
| 5 |
| 2 |
当AP=AB=3时,则PG=
| 32-12 |
| 2 |
| 2 |
同理,当BP=BA=3时,P的坐标是(4-2
| 2 |
故P的坐标是:(
| 5 |
| 2 |
| 2 |
| 2 |
点评:本题考查了待定系数法求一次函数的解析式以及等腰三角形的性质,正确进行讨论是本题的关键.

练习册系列答案
相关题目
光年天文学中的距离单位,1光年大约是9500000000000km,用科学记数法表示为( )
| A、950×1010km |
| B、95×1012km |
| C、9.5×1012km |
| D、0.95×1013km |
 如图,∠MAN=45°,B、C为AN上的两点,且AB=BC=2,D为射线AN上的一个动点,过B、C、D三点作⊙O,则sin∠BDC的最大值为( )
如图,∠MAN=45°,B、C为AN上的两点,且AB=BC=2,D为射线AN上的一个动点,过B、C、D三点作⊙O,则sin∠BDC的最大值为( )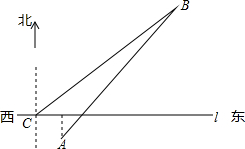 如图,港口A、B位于东西方向航道l的两侧,港口B在A的北偏东45°的方向,航道l上船C与港口B相距100海里,此时在C处测得港口B的方向北偏东55°,已知港口A到航道l距离为13海里,求两港口A、B之间的距离.(参考数据:sin35°≈0.57,cos35°≈0.82,
如图,港口A、B位于东西方向航道l的两侧,港口B在A的北偏东45°的方向,航道l上船C与港口B相距100海里,此时在C处测得港口B的方向北偏东55°,已知港口A到航道l距离为13海里,求两港口A、B之间的距离.(参考数据:sin35°≈0.57,cos35°≈0.82,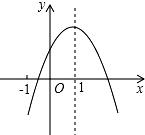 已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,有下列5个结论:①abc<0;②a-b+c>0;③4a+2b+c>0;④2c<3b;⑤a+b<m(am+b)(m≠1的实数),其中正确结论的番号有
已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,有下列5个结论:①abc<0;②a-b+c>0;③4a+2b+c>0;④2c<3b;⑤a+b<m(am+b)(m≠1的实数),其中正确结论的番号有