题目内容
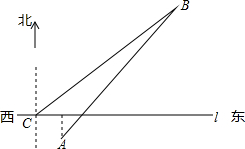 如图,港口A、B位于东西方向航道l的两侧,港口B在A的北偏东45°的方向,航道l上船C与港口B相距100海里,此时在C处测得港口B的方向北偏东55°,已知港口A到航道l距离为13海里,求两港口A、B之间的距离.(参考数据:sin35°≈0.57,cos35°≈0.82,
如图,港口A、B位于东西方向航道l的两侧,港口B在A的北偏东45°的方向,航道l上船C与港口B相距100海里,此时在C处测得港口B的方向北偏东55°,已知港口A到航道l距离为13海里,求两港口A、B之间的距离.(参考数据:sin35°≈0.57,cos35°≈0.82,| 2 |
考点:解直角三角形的应用-方向角问题
专题:
分析:作AD∥l,BD⊥AD于点D,交l于点E,首先在直角三角形CEB中求得BE,然后得到BD的长,最后在直角△BDA中求得AB的长即可.
解答: 解:如图,作AD∥l,BD⊥AD于点D,交l于点E,
解:如图,作AD∥l,BD⊥AD于点D,交l于点E,
由题意得:∠BCE=35°,∠BAD=45°,BC=100海里,
在△BCE中,BE=BC×sin35°=100×0.57=57海里,
∵DE=13海里,
∴BD=57+13=70海里,
∴AB=BD÷sin45°=70
≈99海里.
∴两港口A、B之间的距离是99海里.
 解:如图,作AD∥l,BD⊥AD于点D,交l于点E,
解:如图,作AD∥l,BD⊥AD于点D,交l于点E,由题意得:∠BCE=35°,∠BAD=45°,BC=100海里,
在△BCE中,BE=BC×sin35°=100×0.57=57海里,
∵DE=13海里,
∴BD=57+13=70海里,
∴AB=BD÷sin45°=70
| 2 |
∴两港口A、B之间的距离是99海里.
点评:本题考查了解直角三角形的应用中的方向角问题,解题的关键是从实际问题中抽象出直角三角形,难度不大.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
以下列各组数为边长,能构成直角三角形的是( )
| A、1,2,3 | ||||||
B、
| ||||||
| C、32,42,52 | ||||||
| D、3,4,5 |

 在直角坐标系xOy中,?ABCD四个顶点的坐标分别为A(1,1),B(4,1),C(5,2),D(2,2),直线l:y=kx+b与直线y=-2x平行.
在直角坐标系xOy中,?ABCD四个顶点的坐标分别为A(1,1),B(4,1),C(5,2),D(2,2),直线l:y=kx+b与直线y=-2x平行. 如图,某一时刻一根2米长的竹竿EF影长GE为1.2米,此时,小红测得一颗被风吹斜的柏树与地面成30°角,树顶端B在地面上的影子点D与B到垂直地面的落点C的距离是3.6米,则树长AB是多少米.
如图,某一时刻一根2米长的竹竿EF影长GE为1.2米,此时,小红测得一颗被风吹斜的柏树与地面成30°角,树顶端B在地面上的影子点D与B到垂直地面的落点C的距离是3.6米,则树长AB是多少米. 如图所示,在△ABC中,AD⊥BC于点D,∠B=60°,∠C=45°,BC=20,求AD的长.(结果保留根号)
如图所示,在△ABC中,AD⊥BC于点D,∠B=60°,∠C=45°,BC=20,求AD的长.(结果保留根号)