题目内容
1.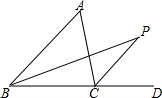 如图.在△ABC中,∠A=α.△ABC的内角平分线与外角平分线交于点P.且∠P=β.试探究图中α与β的关系.并说明理由.
如图.在△ABC中,∠A=α.△ABC的内角平分线与外角平分线交于点P.且∠P=β.试探究图中α与β的关系.并说明理由.
分析 利用角平分线定义可知∠PCD=$\frac{1}{2}$∠ACD.再利用外角性质,可得∠ACD=∠A+∠ABC①,∠PCD=∠P+$\frac{1}{2}$∠ABC②,那么可利用∠PCD=∠P+$\frac{1}{2}$∠ABC,可得相等关系.
解答 解:∵CP是∠ACD的角平分线,
∴∠PCD=$\frac{1}{2}$∠ACD.
又∵∠ACD=∠A+∠ABC,
∴∠PCD=$\frac{1}{2}$∠A+$\frac{1}{2}$∠ABC,
又∵∠PCD=∠P+$\frac{1}{2}$∠ABC,
∴$\frac{1}{2}$∠A+$\frac{1}{2}$∠ABC=∠P+$\frac{1}{2}$∠ABC,
∴∠P=$\frac{1}{2}$∠A,即α=2β.
点评 本题考查的是三角形内角和定理,利用了角平分线定义、三角形外角性质.三角形的外角等于与它不相邻的两个内角之和等知识.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
6.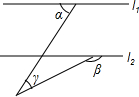 如图,l1∥l2,则下列式子成立的是( )
如图,l1∥l2,则下列式子成立的是( )
 如图,l1∥l2,则下列式子成立的是( )
如图,l1∥l2,则下列式子成立的是( )| A. | ∠α+∠β+∠γ=180° | B. | ∠α+∠β-∠γ=180° | C. | ∠β+∠γ-∠α=180° | D. | ∠α-∠β+∠γ=180° |
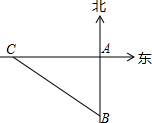 如图,一艘轮船以30km/h的速度沿既定航线由西向东航行,途中接到台风警报,某台风中心正以20km/h的途度由南向北移动,距台风中心200km的圆形区域(包括边界)都属台风影响区.当这艘轮船接到台风警报时,它与台风中心的距离BC=500km,此时台风中心与轮船既定航线的最近距离BA=300km.
如图,一艘轮船以30km/h的速度沿既定航线由西向东航行,途中接到台风警报,某台风中心正以20km/h的途度由南向北移动,距台风中心200km的圆形区域(包括边界)都属台风影响区.当这艘轮船接到台风警报时,它与台风中心的距离BC=500km,此时台风中心与轮船既定航线的最近距离BA=300km.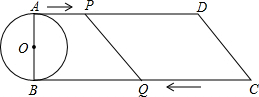 如图,已知直角梯形ABCD中,AD∥BC,∠B=90°,AB=8cm,AD=24cm,BC=26cm,AB为⊙O的直径,动点P从点A开始沿AD边向点D以1cm/s的速度运动,动点Q从点C开始沿CB边向点B以3cm/s速度运动.P、Q分别从点A、C同时出发,当其中一点到达终点时,另一点也随之停止运动,设运动时间为t s,问:
如图,已知直角梯形ABCD中,AD∥BC,∠B=90°,AB=8cm,AD=24cm,BC=26cm,AB为⊙O的直径,动点P从点A开始沿AD边向点D以1cm/s的速度运动,动点Q从点C开始沿CB边向点B以3cm/s速度运动.P、Q分别从点A、C同时出发,当其中一点到达终点时,另一点也随之停止运动,设运动时间为t s,问: