题目内容
14. 如图,是由五个边长为2cm的小立方块搭成的几何体,一只蚂蚁想从A沿着这个几何体的表面爬到点B,它要爬行的最短路程应为2$\sqrt{5}$cm.
如图,是由五个边长为2cm的小立方块搭成的几何体,一只蚂蚁想从A沿着这个几何体的表面爬到点B,它要爬行的最短路程应为2$\sqrt{5}$cm.
分析 根据几何体画展开图,由两点之间,线段最短,构建直角△ABC,根据勾股定理计算可得结论.
解答  解:如图,BC=2,AC=4,
解:如图,BC=2,AC=4,
由勾股定理得:AB=$\sqrt{{2}^{2}+{4}^{2}}$=$\sqrt{20}$=2$\sqrt{5}$,
答:它要爬行的最短路程应为 2$\sqrt{5}$cm.
故答案为:2$\sqrt{5}$.
点评 本题考查了平面展开图的最短路径问题,先根据题意把立体图形展开成平面图形后,再确定两点之间的最短路径.一般情况是两点之间,线段最短.在平面图形上构造直角三角形解决问题.

练习册系列答案
 浙江名校名师金卷系列答案
浙江名校名师金卷系列答案 全优冲刺100分系列答案
全优冲刺100分系列答案
相关题目
2.某校七年级学生到农科所参观,一部分同学骑自行车先走,速度为15km/h,过了40min后,其余同学乘汽车出发,速度是骑自行车同学速度的3倍,设汽车出发xh后追上骑自行车的同学,则下列方程不正确的( )
| A. | 45x=15x+$\frac{2}{3}$×15 | B. | 45x=15x+40×15 | C. | (45-15)x=$\frac{2}{3}$×15 | D. | 45x-$\frac{2}{3}$×15=15x |
9.如下列分数中,能化为有限小数的是( )
| A. | $\frac{1}{3}$ | B. | $\frac{1}{4}$ | C. | $\frac{1}{7}$ | D. | $\frac{1}{9}$ |
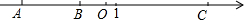 如图,A、B、C是数轴上的三点,O是原点,BO=3,AB=2BO,CO=$\frac{5}{3}$AO.
如图,A、B、C是数轴上的三点,O是原点,BO=3,AB=2BO,CO=$\frac{5}{3}$AO. 某校的围墙上端由一段段相同的凹曲拱形栅栏组成.如图所示,其拱形为抛物线的一部分,栅栏由立柱和横杆用相同的钢筋切割而成,横杆AB间按相同的间距$\frac{1}{5}$米用5根立柱加固,OC的长为$\frac{3}{5}$米.
某校的围墙上端由一段段相同的凹曲拱形栅栏组成.如图所示,其拱形为抛物线的一部分,栅栏由立柱和横杆用相同的钢筋切割而成,横杆AB间按相同的间距$\frac{1}{5}$米用5根立柱加固,OC的长为$\frac{3}{5}$米.