题目内容
16.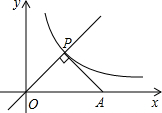 如图,点P是正比例函数y=x与反比例函数y=$\frac{k}{x}$在第一象限内的交点,PA⊥OP交x轴于点A,△POA的面积为3,则k的值是3.
如图,点P是正比例函数y=x与反比例函数y=$\frac{k}{x}$在第一象限内的交点,PA⊥OP交x轴于点A,△POA的面积为3,则k的值是3.
分析 过P作PB⊥OA于B,根据一次函数的性质得到∠POA=45°,则△POA为等腰直角三角形,所以OB=AB,于是S△POB=$\frac{1}{2}$S△POA=$\frac{1}{2}$×3=$\frac{3}{2}$,然后根据反比例函数y=$\frac{k}{x}$(k≠0)系数k的几何意义即可得到k的值.
解答 解:过P作PB⊥OA于B,如图,
∵正比例函数的解析式为y=x,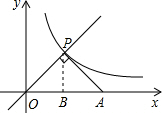
∴∠POA=45°,
∵PA⊥OP,
∴△POA为等腰直角三角形,
∴OB=AB,
∴S△POB=$\frac{1}{2}$S△POA=$\frac{1}{2}$×3=$\frac{3}{2}$,
∴$\frac{1}{2}$k=$\frac{3}{2}$,
∴k=3.
故答案为3.
点评 本题考查了反比例函数y=$\frac{k}{x}$(k≠0)系数k的几何意义:从反比例函数y=$\frac{k}{x}$(k≠0)图象上任意一点向x轴和y轴作垂线,垂线与坐标轴所围成的矩形面积为|k|.也考查了等腰直角三角形的性质.

练习册系列答案
 培优口算题卡系列答案
培优口算题卡系列答案 开心口算题卡系列答案
开心口算题卡系列答案 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案
相关题目
11.用换元法解方程$\frac{y}{{y}^{2}-3}$+$\frac{{y}^{2}-3}{y}$=$\frac{5}{2}$时,如果设x=$\frac{y}{{y}^{2}-3}$,那么原方程可化为( )
| A. | 2x2-5x+2=0 | B. | x2-5x+1=0 | C. | 2x2+5x+2=0 | D. | 2x2-5x+1=0 |
8.下列说法正确的是( )
| A. | 一个游戏的中奖概率是$\frac{1}{100}$,则做100次这样的游戏一定会中奖 | |
| B. | 为了解全国中学生的心理健康情况,应该采用普查的方式 | |
| C. | 一组数据 8,8,7,10,6,8,9 的众数和中位数都是8 | |
| D. | 若甲组数据的方差s2=0.01,乙组数据的方差s2=0.1,则乙组数据比甲组数据稳定 |
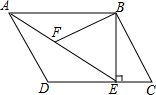 如图,在平行四边形ABCD中,过点B作BE⊥CD,垂足为E,连结AE.F为AE上一点,且∠BFE=∠C.
如图,在平行四边形ABCD中,过点B作BE⊥CD,垂足为E,连结AE.F为AE上一点,且∠BFE=∠C.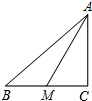 如图,在Rt△ABC中,∠C=90°,AM是BC边上的中线,cos∠CAM=$\frac{4}{5}$,则tan∠B的值为$\frac{2}{3}$.
如图,在Rt△ABC中,∠C=90°,AM是BC边上的中线,cos∠CAM=$\frac{4}{5}$,则tan∠B的值为$\frac{2}{3}$. 如图,在△ABC中,∠BAC=50°,BD、CE分别是边AC,AB上的高,BD、CE相交于点O,则∠BOC的度数是130°.
如图,在△ABC中,∠BAC=50°,BD、CE分别是边AC,AB上的高,BD、CE相交于点O,则∠BOC的度数是130°.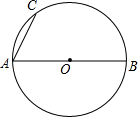 如图,AB是⊙O的直径,AC为弦.
如图,AB是⊙O的直径,AC为弦.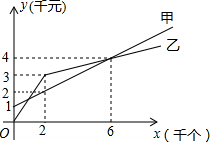 某单位准备印制一批证书,现有两个印刷厂可供选择,甲厂费用分为制版费和印刷费两部分先收取固定的制版费,再按印刷数量收取印刷费,
某单位准备印制一批证书,现有两个印刷厂可供选择,甲厂费用分为制版费和印刷费两部分先收取固定的制版费,再按印刷数量收取印刷费,