题目内容
13.(1)分解因式:a2-1+b2-2ab(2)解方程:$\frac{x-2}{x+2}$=$\frac{x+2}{x-2}$+$\frac{16}{{x}^{2}-4}$
(3)先化简,再求值:$\frac{{m}^{2}-2m+1}{{m}^{2}-1}$÷(m-1-$\frac{m-1}{m+1}$),其中m=$\sqrt{3}$.
分析 (1)根据完全平方公式与平方差公式进行因式分解即可;
(2)先把分式方程化为整式方程,求出x的值,再代入最简公分母进行检验即可;
(3)先算括号里面的,再算除法,最后把m的值代入进行计算即可.
解答 解:(1)原式=(a-b)2-1=(a-b-1)(a-b+1);
(2)方程的两边同时乘以x2-4得,
(x-2)2=(x+2)2+16,解得x=-2,
经检验x=-2是原分式方程的增根,故原分式方程无解;
(3)原式=$\frac{m-1}{m+1}$÷$\frac{{m}^{2}-1-m+1}{m+1}$
=$\frac{m-1}{m+1}$÷$\frac{m(m-1)}{m+1}$
=$\frac{m-1}{m+1}$•$\frac{m+1}{m(m-1)}$
=$\frac{1}{m}$,
当m=$\sqrt{3}$时,原式=$\frac{\sqrt{3}}{3}$.
点评 本题考查的是分式的化简求值,此类题型的特点是:利用方程解的定义找到相等关系,再把所求的代数式化简后整理出所找到的相等关系的形式,再把此相等关系整体代入所求代数式,即可求出代数式的值.

练习册系列答案
 阶梯计算系列答案
阶梯计算系列答案
相关题目
 如图,点A、B在数轴上,它们所对应的数分别是-2与$\frac{2x+2}{3x-5}$,且点A、B到原点的距离相等,求x的值.
如图,点A、B在数轴上,它们所对应的数分别是-2与$\frac{2x+2}{3x-5}$,且点A、B到原点的距离相等,求x的值.
 如图,在平面直角坐标系中,原点为O,点A(0,3),B(2,3),C(2,-3),D(0,-3).点P,Q是长方形ABCD边上的两个动点,BC交x轴于点M.点P从点O出发以每秒1个单位长度沿O→A→B→M的路线做匀速运动,同时点Q也从点O出发以每秒2个单位长度沿O→D→C→M的路线做匀速运动.当点Q运动到点M时,两动点均停止运动.设运动的时间为t秒,四边形OPMQ的面积为S.
如图,在平面直角坐标系中,原点为O,点A(0,3),B(2,3),C(2,-3),D(0,-3).点P,Q是长方形ABCD边上的两个动点,BC交x轴于点M.点P从点O出发以每秒1个单位长度沿O→A→B→M的路线做匀速运动,同时点Q也从点O出发以每秒2个单位长度沿O→D→C→M的路线做匀速运动.当点Q运动到点M时,两动点均停止运动.设运动的时间为t秒,四边形OPMQ的面积为S.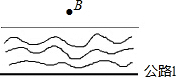 如图,河边有一条笔直的公路l,公路两侧是平坦的草地,在数学活动课上,老师要求测量河对岸B点到公路的距离,请你设计一个测量方案.要求:
如图,河边有一条笔直的公路l,公路两侧是平坦的草地,在数学活动课上,老师要求测量河对岸B点到公路的距离,请你设计一个测量方案.要求: 如图,在图中求作⊙P,使得⊙P经过点M与点N,且圆心P到∠AOB两边的距离相等(要求:尺规作图,不写作法,保留作图痕迹,并把作图痕迹用黑色签字笔加黑).
如图,在图中求作⊙P,使得⊙P经过点M与点N,且圆心P到∠AOB两边的距离相等(要求:尺规作图,不写作法,保留作图痕迹,并把作图痕迹用黑色签字笔加黑).