Question

1．如图，在平面直角坐标系中，原点为O，点A（0，3），B（2，3），C（2，-3），D（0，-3）．点P，Q是长方形ABCD边上的两个动点，BC交x轴于点M．点P从点O出发以每秒1个单位长度沿O→A→B→M的路线做匀速运动，同时点Q也从点O出发以每秒2个单位长度沿O→D→C→M的路线做匀速运动．当点Q运动到点M时，两动点均停止运动．设运动的时间为t秒，四边形OPMQ的面积为S．
（1）当t=2时，求S的值；
（2）若S＜5时，求t的取值范围．

Answer 1

分析 设三角形OPM的面积为S₁，三角形OQM的面积为S₂，则S=S₁+S₂．
（1）当t=2时，可得点P（0，2），Q（1，-3），过点Q作QE⊥x轴于点E．根据三角形的面积公式分别求出S₁，S₂，进而得出S的值；
（2）设点P运动的路程为t，则点Q运动的路程为2t．分五种情况进行讨论：①0＜t≤1.5；②1.5＜t≤2.5；③2.5＜t≤3； ④3＜t＜4；⑤t=4．针对每一种情况，首先确定出对应范围内点P，Q的位置，再根据三角形的面积公式求解即可．

解答 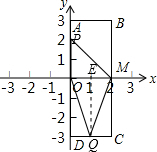解：设三角形OPM的面积为S₁，三角形OQM的面积为S₂，则S=S₁+S₂．
（1）当t=2时，点P（0，2），Q（1，-3），过点Q作QE⊥x轴于点E．
∵S₁=$\frac{1}{2}$OP•OM=$\frac{1}{2}$×2×2=2，
S₂=$\frac{1}{2}$QE•OM=$\frac{1}{2}$×3×2=3，
∴S=S₁+S₂=5；

（2）设点P运动的路程为t，则点Q运动的路程为2t．
①当0＜t≤1.5时，点P在线段OA上，点Q在线段OD上，
此时四边形OPMQ不存在，不合题意，舍去．
②当1.5＜t≤2.5时，点P在线段OA上，点Q在线段DC上．
S=$\frac{1}{2}$×2t+$\frac{1}{2}$×2×3=t+3，
∵S＜5，
∴t+3＜5，解得t＜2．
此时1.5＜t＜2．
 ③当2.5＜t≤3时，点P在线段OA上，点Q在线段CM上．
S=$\frac{1}{2}$×2t+$\frac{1}{2}$×2（8-2t）=8-t，
∵S＜5，
∴8-t＜5，解得t＞3．
 ④当3＜t＜4时，点P在线段AB上，点Q在线段CM上．
S=$\frac{1}{2}$×2×3+$\frac{1}{2}$×2（8-2t）=11-2t，
∵S＜5，
∴11-2t＜5，解得t＞3．
此时3＜t＜4．
 ⑤当t=4时，点P是线段AB的中点，点Q与M重合，两动点均停止运动．
此时四边形OPMQ不存在，不合题意，舍去．
综上所述，当S＜5时，1.5＜t＜2或3＜t＜4．

点评 本题考查了坐标与图形性质，三角形、四边形的面积，确定点P，Q的位置是解决第（1）问的关键；正确进行分类，考虑到所有可能的情况是解决第（2）问的关键．