Question

6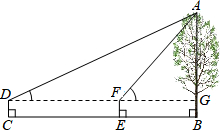．如图，小明同学用仪器测量一棵大树AB的高度，在C处测得∠ADG=30°，在E处测得∠AFG=60°，CE=8米，仪器高度CD=1.4米．
（精确到个位，参考数据：$\sqrt{2}$≈1.41，$\sqrt{3}$≈1.73，$\sqrt{5}$≈2.23）
（1）求AF的长度；
（2）求这棵树AB的高度．

Answer 1

分析 首先根据题意可得GB=EF=CD=1.5米，DF=CE=8米，然后设AG=x米，GF=y米，则在Rt△AFG与Rt△ADG，利用正切函数，即可求得x与y的关系，解方程组即可求得答案

解答 解：根据题意得，四边形DCEF、DCBG是矩形，
∴GB=EF=CD=1.5米，DF=CE=8米，
设AG=x米，GF=y米，
在Rt△AFG中，tan∠AFG=tan60°=$\frac{AG}{FG}$=$\frac{x}{y}$=$\sqrt{3}$，
在Rt△ADG中，tan∠ADG=tan30°=$\frac{AG}{DG}$=$\frac{x}{y+8}$=$\frac{\sqrt{3}}{3}$，
∴x=4$\sqrt{3}$，y=4，即AG=4$\sqrt{3}$米，FG=4米．
（1）AF=$\sqrt{A{G}^{2}+F{G}^{2}}$=8（米）；

（2）则AB=AG+GB=4$\sqrt{3}$+1.4≈8（米）．
答：这棵树AB的高度约为8米．

点评 本题考查了解直角三角形的应用，注意能借助仰角构造直角三角形并解直角三角形是解此题的关键，注意数形结合思想与方程思想的应用．