题目内容
14. 如图,正方形ABCD的边长为6,点E在边AB上,连接ED,过点D作FD⊥DE与BC的延长线相交于点F,连接EF与边CD相交于点G,与对角线BD相交于点H.若BD=BF,求BE的长.
如图,正方形ABCD的边长为6,点E在边AB上,连接ED,过点D作FD⊥DE与BC的延长线相交于点F,连接EF与边CD相交于点G,与对角线BD相交于点H.若BD=BF,求BE的长.
分析 由四边形ABCD正方形,BF=BD=6 $\sqrt{2}$,由DF⊥DE,易证得△ADE≌△CDF,即可求得BE的长;
解答 解:如图,∵在正方形ABCD中,∠BCD=90°,BC=CD=6,
∴BD=6 $\sqrt{2}$.
∵DF⊥DE,
∴∠ADE+∠EDC=90°,∠EDC+∠CDF=90°,
∴∠ADE=∠CDF,
在△ADE和△CDF中,
$\left\{\begin{array}{l}{∠ADE=∠CDF}\\{AD=DC}\\{∠A=∠DCF=90°}\end{array}\right.$,
∴△ADE≌△CDF(ASA),
∴AE=CF.
又∵BD=BF=6 $\sqrt{2}$,
∴AE=CF=BF-BC=6 $\sqrt{2}$-6,
∴BE=AB-AE=6-(6 $\sqrt{2}$-6)=12-6 $\sqrt{2}$,即BE的长为12-6 $\sqrt{2}$;
点评 此题考查了正方形的性质、全等三角形的判定与性质、等腰直角三角形的性质以及等边三角形的判定与性质.此题综合性较强,难度较大,注意掌握辅助线的作法,注意数形结合思想的应用.

练习册系列答案
相关题目
4.为了缓解城市用水紧张及提倡节约用水,某市自2017年1月1日起调整居民用水价格,每立方米水费上涨25%.该市林老师家2016年12月份的水费是18元,而2017年1月份的水费是36元,且已知林老师家2017年1月份的用水量比2016年12月份的用水量多6m3.求该市去年的居民用水价格?设去年的居民用水价格x元/m3,则所列方程正确的是( )
| A. | $\frac{18}{1.25x}$-$\frac{36}{x}$=6 | B. | $\frac{36}{1.25x}$-$\frac{18}{x}$=6 | C. | $\frac{36}{x}$-$\frac{18}{1.25x}$=6 | D. | $\frac{18}{x}$-$\frac{36}{1.25x}$=6 |
19.化简$\frac{4}{x-4}$+$\frac{x}{4-x}$的结果是( )
| A. | -1 | B. | 1 | C. | -3 | D. | 3 |
 如图,正方形ABCD中,E为对角线BD上一点,过E点作EF⊥BC,EH⊥AE,MN⊥BD,求证:EN=$\frac{1}{2}$BD.
如图,正方形ABCD中,E为对角线BD上一点,过E点作EF⊥BC,EH⊥AE,MN⊥BD,求证:EN=$\frac{1}{2}$BD.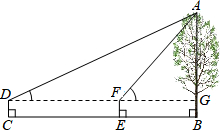 如图,小明同学用仪器测量一棵大树AB的高度,在C处测得∠ADG=30°,在E处测得∠AFG=60°,CE=8米,仪器高度CD=1.4米.
如图,小明同学用仪器测量一棵大树AB的高度,在C处测得∠ADG=30°,在E处测得∠AFG=60°,CE=8米,仪器高度CD=1.4米.