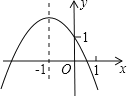Question

【题目】在平面直角坐标系中，已知点，，直线与轴和轴分别交于点，，若抛物线与直线有两个不同的交点，其中一个交点在线段上（包含，两个端点），另一个交点在线段上（包含，两个端点），则的取值范围是

A. B. 或C. D. 或

Answer 1

【答案】C

【解析】

根据待定系数法求出直线AB解析式，求出点M,N的坐标，根据一次函数以及二次函数的增减性，要使抛物线与直线有两个不同的交点，其中一个交点在线段上（包含，两个端点），另一个交点在线段上（包含，两个端点）成立，则需①、②、③ 、④同时成立，解不等式组即可.

设直线AB的解析式为，由题意得

解得

直线AB的解析式为，当时，；当时，.

在中，当时，.

中, ，中，抛物线开口向上，

要使抛物线与直线AB有两个不同的交点，其中一个交点在线段AN上（包含A，N两个端点），另一个交点在线段BM上（包含B，M两个端点），需

①、②、③ 、④同时成立.

解①得，；②成立；解③得；解④得.

综上，.

故选：C.