Question

【题目】已知，如图，抛物线与轴交点坐标为，

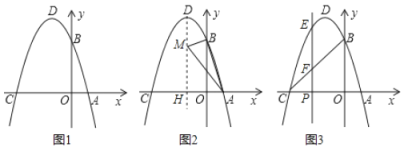
（1）如图1，已知顶点坐标为或点，选择适当方法求抛物线的解析式；

（2）如图2，在（1）的条件下，在抛物线的对称轴上求作一点，使的周长最小，并求出点的坐标；

（3）如图3，在（1）的条件下，将图2中的对称轴向左移动，交轴于点，与抛物线，线段的交点分别为点、，用含的代数式表示线段的长度，并求出当为何值时，线段最长．

Answer 1

【答案】（1）；（2）点坐标为；（3）

【解析】

（1）根据顶点坐标设顶点式，将点的坐标代入顶点式解未知系数即得．

（2）先确定的周长最小为BC的长度，再用待定系数法求BC的解析式，最后根据M点横坐标确定纵坐标即得．

（3）先用m表示E点和F点的坐标，再利用两点纵坐标之差将线段EF的长度用m表示，最后建立线段EF的长度与m之间的函数关系并将解析式化为顶点式即得．

解：（1）由抛物线的顶点的坐标可设其解析式为，

将点代入，得：，

解得，则抛物线解析式为；

（2）如图：连接，交于点

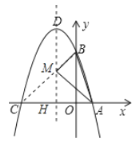
∵A点与C点关于对称轴对称

∴

∵两点之间线段最短

∴的周长最小为BC的长度

设直线的解析式为，

将，代入得，，

解得：

∴直线的解析式为

当时，

∴点坐标为；

（3）由题意知，，

则，

∴当时，线段最长．