Question

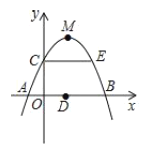
【题目】如图，已知抛物线过点，顶点为M，与x轴交于AB两点，D为AB的中点，轴，交抛物线于点E，下列结论中正确的是（ ）

A.抛物线的对称轴是直线x=-3B.

C.D.四边形ADEC是菱形

Answer 1

【答案】C

【解析】

由顶点坐标可判断A选项；

求出函数解析式，继而求出点A坐标，求出AD、CD的长，可判断B选项；

求出CD、CM、MD的长，利用勾股定理的逆定理可判断C选项；

根据AD与CE位置关系和数量关系可判断是否为平行四边形，根据AD与AC的数量关系可判断邻边是否相等，由此可判断D选项.

解：A. 抛物线的对称轴是直线x=3，故此选项错误；

B.把x=0，y=4代入得a= ；

∴，

当y=0时，，

解得，

∴点A的坐标为（-2，0）

由题意可知，C（0，4），D（3，0），
∴CD=5，AD=3-（-2）=5，

∴CD= AD，

故B选项错误；

C.由题意M（3，），C（0，4），D（3，0），
∴OC=4，OD=3，
∴CD=5，CM= ，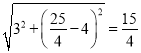

∴CD2+CM2=DM2，
∴∠MCD=90°，

故C选项正确；

D．∵C（0，4），抛物线的对称轴是直线x=3，轴，

∴E的坐标是（6，4），

∴CE=6，

∵AD=5，

∴CE AD，

∴四边形ADEC不是平行四边形，

∴四边形ADEC不是菱形，

故D选项错误.
故选：C．