题目内容
【题目】在![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() ,分别交直线
,分别交直线![]() 、
、![]() 于点
于点![]() 、
、![]() .
.
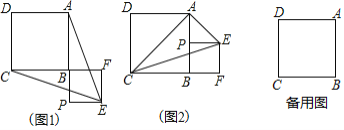
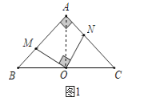
(1)如图1,当![]() 时,求证:
时,求证:![]() ;
;
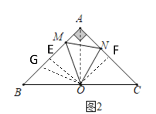
(2)如图2,当![]() 时,线段
时,线段![]() 、
、![]() 、
、![]() 之间有何数量关系,证明你的结论;
之间有何数量关系,证明你的结论;
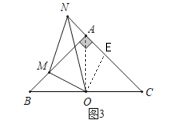
(3)如图3,当![]() 时,旋转
时,旋转![]() ,问线段之间
,问线段之间![]() 、
、![]() 、
、![]() 有何数量关系?证明你的结论.
有何数量关系?证明你的结论.
【答案】(1)见解析;(2)![]() ,证明见解析;(3)
,证明见解析;(3)![]() ,证明见解析
,证明见解析
【解析】
(1)根据等腰直角三角形的性质可得![]() ,
,![]() ,
,![]() ,然后利用ASA证出
,然后利用ASA证出![]() ,从而证出结论;
,从而证出结论;
(2)过![]() 作
作![]() ,
,![]() ,连接AO,证出
,连接AO,证出![]() ,AO平分∠BAC,
,AO平分∠BAC,![]() ,从而得出OE=OF,BE=OE,将△ONF逆时针旋转,使OF和OE重合,点N落在点G处,利用SAS即可证出△MOG≌△MON,得出MN =GM,再结合正方形的性质和等量代换即可得出结论;
,从而得出OE=OF,BE=OE,将△ONF逆时针旋转,使OF和OE重合,点N落在点G处,利用SAS即可证出△MOG≌△MON,得出MN =GM,再结合正方形的性质和等量代换即可得出结论;
(3)在![]() 上截取
上截取![]() ,连接
,连接![]() ,先利用SAS证出
,先利用SAS证出![]() ,从而得出
,从而得出![]() ,
,![]() ,再利用SAS证出
,再利用SAS证出![]() ,最后利用等量代换即可得出结论.
,最后利用等量代换即可得出结论.
证明:(1)∵![]() ,
,![]() ,
,![]() ,
,
∴![]() ,
,![]() ,
,![]()
∵![]() ,
,
∴∠AOM+∠AON=90°,∠CON+∠AON=90°
∴![]()
在△AOM和△CON中
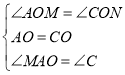
∴![]() ,
,
∴![]()
(2)![]() 、
、![]() 、
、![]() 之间的数量关系是:
之间的数量关系是:![]()
过![]() 作
作![]() ,
,![]() ,连接AO
,连接AO
∴四边形![]() 为矩形
为矩形
∵![]() ,
,![]() ,
,![]()
∴![]() ,AO平分∠BAC,
,AO平分∠BAC,![]()
∴OE=OF,BE=OE
∴四边形![]() 为正方形,
为正方形,
∵![]()
将△ONF逆时针旋转,使OF和OE重合,点N落在点G处
∴∠MOG=∠EOM+∠NOF=90°-∠MON=45°=![]() ,OG=ON,GE=FN
,OG=ON,GE=FN
在△MOG和△MON中
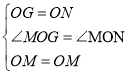
∴△MOG≌△MON
∴MN =GM=EM+GE=![]()
∴![]()
而![]()
∴![]()
(3)![]()
在![]() 上截取
上截取![]() ,连接
,连接![]()
∵![]() ,
,![]() ,
,![]() ,
,
∴![]() ,
,![]() ,
,
在△BOM和△AOE中
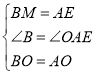
∴![]() ,
,
∴![]() ,
,![]()
∵![]() ,
,
∴![]()
即![]() ,
,
在△MON和△EON中
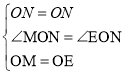
∴![]()
∴![]()

练习册系列答案
相关题目