题目内容
11. 如图,△ABC的内切圆O与各边分别相切于D,E,F三点,则点O是△DEF的( )
如图,△ABC的内切圆O与各边分别相切于D,E,F三点,则点O是△DEF的( )| A. | 三条中线的交点 | B. | 三条高的交点 | ||
| C. | 三条角平分线的交点 | D. | 三条边的垂直平分线的交点 |
分析 连接OE、OF、OD,根据切线的性质得到OE⊥AB,OF⊥AC,OD⊥BC,根据圆的半径的性质得到OE=OF=OD,根据角平分线的判定定理解答.
解答 解: 连接OE、OF、OD,
连接OE、OF、OD,
∵△ABC的内切圆O与各边分别相切于D,E,F三点,
∴OE⊥AB,OF⊥AC,OD⊥BC,OE=OF=OD,
即点O到△DEF的三个顶点的距离相等,
∴点O是△DEF的三条边的垂直平分线的交点,
故选:D.
点评 本题考查的是三角形的内切圆和内心的概念和性质,掌握三角形的内切圆的性质、角平分线的判定定理是解题的关键.

练习册系列答案
 寒假大串联黄山书社系列答案
寒假大串联黄山书社系列答案
相关题目
1.下列方程中,变形正确的是( )
| A. | 若$\frac{1}{2}$x=x-1,则x=2x-1 | B. | 若$\frac{1}{3}$x=2,则x=$\frac{2}{3}$ | ||
| C. | 若3x-1=x+2,则3x-x=2+1 | D. | 若2(x-2)=5,则2x=5-4 |
2.下列奥运会徽中,中心对称图形是( )
| A. |  | B. |  | C. |  | D. |  |
10.已知二元一次方程5x-6y=20,当y<0时,x的取值范围是( )
| A. | x>4 | B. | x<4 | C. | x>-4 | D. | x<-4 |


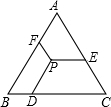 如图,P是等边三角形ABC内任一点,过点P作PD∥AB,PE∥BC,PF∥AC,分别交BC、AC、AB于点D、E、F.求证:PD+PE+PF=BC.
如图,P是等边三角形ABC内任一点,过点P作PD∥AB,PE∥BC,PF∥AC,分别交BC、AC、AB于点D、E、F.求证:PD+PE+PF=BC.