题目内容
8. 如图所示,△ABC中,DE∥BC,若$\frac{AD}{DB}$=$\frac{1}{2}$,则下列结论中错误的是( )
如图所示,△ABC中,DE∥BC,若$\frac{AD}{DB}$=$\frac{1}{2}$,则下列结论中错误的是( )| A. | $\frac{AE}{EC}$=$\frac{1}{2}$ | B. | $\frac{{S}_{△ADE}}{{S}_{△ABC}}$=$\frac{1}{9}$ | ||
| C. | $\frac{DE}{BC}$=$\frac{1}{2}$ | D. | $\frac{△ADE的周长}{△ABC的周长}$=$\frac{1}{3}$ |
分析 根据平行线的性质以及相似三角形的性质即可作出判断.
解答 解: ∵DE∥BC,
∵DE∥BC,
∴△ADE∽△ABC,$\frac{AD}{DB}$=$\frac{AE}{EC}$=$\frac{1}{2}$,故A正确,
∴$\frac{AD}{AB}$=$\frac{DE}{BC}$=$\frac{AE}{AC}$,
∵$\frac{AD}{DB}$=$\frac{1}{2}$,
∴$\frac{AD}{AB}$=$\frac{DE}{BC}$=$\frac{AE}{AC}$=$\frac{1}{3}$,$\frac{{S}_{△ADE}}{{S}_{△ABC}}$=$\frac{1}{9}$,$\frac{△ADE的周长}{△ABC的周长}$=$\frac{1}{3}$,故B、D正确.
故选C.
点评 本题考查相似三角形的判定和性质、平行线分线段成比例定理,解题的关键是记住相似三角形的面积比等于相似比的平方,周长比等于相似比,属于中考常考题型.

练习册系列答案
相关题目
19.下列运算正确的是( )
| A. | -2(a-1)=-2a+1 | B. | (x3y)2=x5y2 | C. | x8÷x2=x6 | D. | (x+3)2=x2+9 |
20.不等式2x<-6的解集为( )
| A. | x<-3 | B. | x>-3 | C. | x>3 | D. | x<3 |
17.中国倡导的“一带一路”建设将促进我国与世界各国的互利合作,根据规划,“一带一路”地区覆盖总人口约为4600000000人,这个数用科学记数法表示为( )
| A. | 46×108 | B. | 4.6×109 | C. | 4.6×10-9 | D. | 4.6×1010 |
 如图,以AB为直径的⊙O经过AC的中点D,DE⊥BC于点E,若DE=1,∠C=30°,则图中阴影部分的面积是$\frac{4}{9}$π-$\frac{\sqrt{3}}{3}$.
如图,以AB为直径的⊙O经过AC的中点D,DE⊥BC于点E,若DE=1,∠C=30°,则图中阴影部分的面积是$\frac{4}{9}$π-$\frac{\sqrt{3}}{3}$.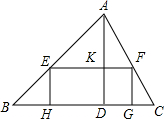 如图,已知锐角△ABC中,边BC长为90,高AD长为60,矩形EFGH的边GH在BC边上,其余两个顶点E,F分别在AB,AC上,EF交AD于点K.
如图,已知锐角△ABC中,边BC长为90,高AD长为60,矩形EFGH的边GH在BC边上,其余两个顶点E,F分别在AB,AC上,EF交AD于点K.