题目内容
13.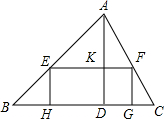 如图,已知锐角△ABC中,边BC长为90,高AD长为60,矩形EFGH的边GH在BC边上,其余两个顶点E,F分别在AB,AC上,EF交AD于点K.
如图,已知锐角△ABC中,边BC长为90,高AD长为60,矩形EFGH的边GH在BC边上,其余两个顶点E,F分别在AB,AC上,EF交AD于点K.(1)求$\frac{AK}{EF}$的值;
(2)设EH=x,矩形EFGH的面积为y,求y与x的函数关系式,并求y的最大值.
分析 (1)根据相似三角形性质:相似比等于对应边上的高的比,即可解决问题.
(2)利用(1)的结论,构建二次函数,利用二次函数的最值问题即可解决.
解答 解:(1) ∵四边形EFGH是矩形,
∵四边形EFGH是矩形,
∴EF∥BC,
∴△AEF∽△ABC
∵AD⊥BC,
∴AD⊥EF,
∴$\frac{EF}{BC}$=$\frac{AK}{AD}$,∵AD=60,BC=90,
∴$\frac{AK}{EF}$=$\frac{AD}{BC}$=$\frac{60}{90}$=$\frac{2}{3}$.
(2)由(1)可知$\frac{EF}{BC}$=$\frac{AK}{AD}$,
∴EF=$\frac{90•(60-x)}{60}$=90-$\frac{3}{2}$x,
∴y=-$\frac{3}{2}$x2+90x=-$\frac{3}{2}$(x-30)2+1350.
∵a=-$\frac{3}{2}$<O,
∴x=30时,y最大值=1350.
点评 本题考查相似三角形的性质、矩形的性质、二次函数的性质等知识,解题的关键是掌握相似三角形的对应边的比等于对应边上的高的比,学会构建二次函数解决最值问题,属于中考常考题型.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
8. 如图所示,△ABC中,DE∥BC,若$\frac{AD}{DB}$=$\frac{1}{2}$,则下列结论中错误的是( )
如图所示,△ABC中,DE∥BC,若$\frac{AD}{DB}$=$\frac{1}{2}$,则下列结论中错误的是( )
 如图所示,△ABC中,DE∥BC,若$\frac{AD}{DB}$=$\frac{1}{2}$,则下列结论中错误的是( )
如图所示,△ABC中,DE∥BC,若$\frac{AD}{DB}$=$\frac{1}{2}$,则下列结论中错误的是( )| A. | $\frac{AE}{EC}$=$\frac{1}{2}$ | B. | $\frac{{S}_{△ADE}}{{S}_{△ABC}}$=$\frac{1}{9}$ | ||
| C. | $\frac{DE}{BC}$=$\frac{1}{2}$ | D. | $\frac{△ADE的周长}{△ABC的周长}$=$\frac{1}{3}$ |
 如图,已知AB=AC,DE垂直平分AB,若∠A=40°,则∠EBC=30°.
如图,已知AB=AC,DE垂直平分AB,若∠A=40°,则∠EBC=30°.
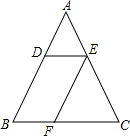 如图,△ABC中,AB=AC,点D在AB上,过点D作BC的平行线,与AC相交于点E,点F在BC上,EF=EC.求证:四边形DBFE是平行四边形.
如图,△ABC中,AB=AC,点D在AB上,过点D作BC的平行线,与AC相交于点E,点F在BC上,EF=EC.求证:四边形DBFE是平行四边形.