题目内容
18.在一个箱子中有三个分别标有数字1,2,3的材质、大小都相同的小球,从中任意摸出一个小球,记下小球的数字x后,放回箱中并摇匀,再摸出一个小球,又记下小球的数字y.以先后记下的两个数字(x,y)作为点P的坐标.(1)求点P的横坐标与纵坐标的和为4的概率;
(2)求点P落在以坐标原点为圆心、$\sqrt{10}$为半径的圆的内部的概率.
分析 (1)首先根据题意列出表格,然后根据表格即可求得点M坐标的所有可能的结果,然后利用概率公式求解即可;
(2)确定满足条件的点的个数,利用概率公式求解,即可求得答案.
解答 解:(1)列表得:
| 1 | 2 | 3 | |
| 1 | (1,1) | (1,2) | (1,3) |
| 2 | (2,1) | (2,2) | (2,3) |
| 3 | (3,1) | (3,2) | (3,3) |
故P(和为4)=$\frac{3}{9}$=$\frac{1}{3}$.
(2)因为点M在以坐标原点为圆心,以$\sqrt{10}$为半径的圆的内部,
所以x2+y2<10,这样的点M有4种形式:(1,1)、(1,2)、(2,1)、(2,2),
所以点M在以坐标原点为圆心,以$\sqrt{10}$为半径的圆的内部的概率P=$\frac{4}{9}$.
点评 考查概率的求法;用到的知识点为:概率=所求情况数与总情况数之比.正确的列表或树状图是解答本题的关键,难度不大.

练习册系列答案
 中考利剑中考试卷汇编系列答案
中考利剑中考试卷汇编系列答案 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案
相关题目
8.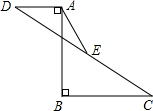 如图,已知AB=12,AB⊥BC于B,AB⊥AD于A,AD=5,BC=10.点E是CD的中点,则AE的长为( )
如图,已知AB=12,AB⊥BC于B,AB⊥AD于A,AD=5,BC=10.点E是CD的中点,则AE的长为( )
 如图,已知AB=12,AB⊥BC于B,AB⊥AD于A,AD=5,BC=10.点E是CD的中点,则AE的长为( )
如图,已知AB=12,AB⊥BC于B,AB⊥AD于A,AD=5,BC=10.点E是CD的中点,则AE的长为( )| A. | 6 | B. | $\frac{13}{2}$ | C. | 5 | D. | $\frac{3}{2}$$\sqrt{41}$ |
 如图,已知E、F是平行四边形ABCD对角线AC上的两点,且BE⊥AC,DF⊥AC.求证:△ABE≌△CDF.
如图,已知E、F是平行四边形ABCD对角线AC上的两点,且BE⊥AC,DF⊥AC.求证:△ABE≌△CDF.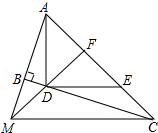 如图,∠ABC=90°,D、E分别在BC、AC上,AD⊥DE,且AD=DE,点F是AE的中点,延长AB交FD的延长线于点M,连接MC.
如图,∠ABC=90°,D、E分别在BC、AC上,AD⊥DE,且AD=DE,点F是AE的中点,延长AB交FD的延长线于点M,连接MC. 如图,某人将一块正五边形玻璃打碎成四块,现要到玻璃店配一块完全一样的玻璃,那么最省事的方法是带①块.
如图,某人将一块正五边形玻璃打碎成四块,现要到玻璃店配一块完全一样的玻璃,那么最省事的方法是带①块.