题目内容
3.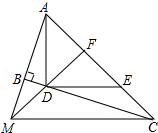 如图,∠ABC=90°,D、E分别在BC、AC上,AD⊥DE,且AD=DE,点F是AE的中点,延长AB交FD的延长线于点M,连接MC.
如图,∠ABC=90°,D、E分别在BC、AC上,AD⊥DE,且AD=DE,点F是AE的中点,延长AB交FD的延长线于点M,连接MC.求证:FM=FC.
分析 如图,首先证明DF⊥AE,DF=AF=EF,这是解决问题的关键性结论;运用AAS公理证明△DFC≌△AFM,得到MF=CF,即可解决问题.
解答  证明:∵△ADE是等腰直角三角形,F是AE中点,
证明:∵△ADE是等腰直角三角形,F是AE中点,
∴DF⊥AE,DF=AF=EF;
又∵∠ABC=90°,∠DCF,∠AMF都与∠MAC互余,
∴∠DCF=∠AMF;在△DFC与△AFM中,
$\left\{\begin{array}{l}{∠DFC=∠AFM}\\{∠DCF=∠AMF}\\{DF=AF}\end{array}\right.$,
∴△DFC≌△AFM(AAS),
∴MF=CF.
点评 该题主要考查了直角三角形的性质、全等三角形的判定等几何知识点及其应用问题;牢固掌握全等三角形的判定等几何知识点是灵活运用、解题的基础和关键.

练习册系列答案
相关题目
14.下面图形不是轴对称图形的是( )
| A. | 等腰三角形 | B. | 菱形 | C. | 平行四边形 | D. | 正六边形 |
15.下列运算正确的是( )
| A. | a3+a4=a7 | B. | (2a4)3=8a7 | C. | 2a3•a4=2a7 | D. | a8÷a2=a4 |
12.-$\frac{2}{5}$的绝对值是( )
| A. | $\frac{5}{2}$ | B. | -$\frac{5}{2}$ | C. | $\frac{2}{5}$ | D. | -$\frac{2}{5}$ |
 二次函数y=ax2+bx+c(a≠0)的图象如图,若|ax2+bx+c|=k(k≠0)有两个不相等的实数根,则k的取值范围是k>3.
二次函数y=ax2+bx+c(a≠0)的图象如图,若|ax2+bx+c|=k(k≠0)有两个不相等的实数根,则k的取值范围是k>3.