题目内容
14. 如图,⊙O中,弦AD=BC.
如图,⊙O中,弦AD=BC.(1)求证:AC=BD.
(2)若∠D=60°,⊙O的半径为2,求弧AB的长.
分析 (1)由在同圆中,弦相等,则所对的弧相等和等量加等量还是等量求解;
(2)根据同弧所对的圆周角等于所对圆心角的一半,得出弧AB所对的圆心角,再由弧长公式计算即可.
解答 证明:(1)∵AD=BC,
∴$\widehat{AD}$=$\widehat{BC}$.
∴$\widehat{AD}$+$\widehat{CD}$=$\widehat{BC}$+$\widehat{CD}$.
∴$\widehat{AC}$=$\widehat{BD}$.
∴AC=BD;
(2)∵∠D=60°,
∴弧AB所对的圆心角=120°,
∴l=$\frac{nπr}{180°}$=$\frac{120π×2}{180}$=$\frac{4}{3}$π,
∴弧AB的长为$\frac{4}{3}$π.
点评 本题考查了弧、弦、圆心角以及弧长的计算,熟练掌握圆周角定理和弧长公式是解题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
4.下列事件中,属于不可能事件的是( )
| A. | 明天某地区早晨有雾 | |
| B. | 抛掷一枚质地均匀的骰子,向上一面的点数是6 | |
| C. | 声音可以在真空中传播 | |
| D. | 明天见到的第一辆公交车的牌照的末位数字将是偶数 |
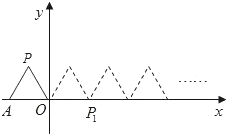 如图,将边长为1的正△OAP沿x轴正方向连续翻转,△OAP第1次翻转后记为△O1A1P1,第2次翻转后记为△O2A2P2,…,如果经过若干次翻转后点P的横坐标是2014,则翻转次数为2014或2015.
如图,将边长为1的正△OAP沿x轴正方向连续翻转,△OAP第1次翻转后记为△O1A1P1,第2次翻转后记为△O2A2P2,…,如果经过若干次翻转后点P的横坐标是2014,则翻转次数为2014或2015. 如图,△ABC≌△DBC,∠A=110°,则∠D=110°.
如图,△ABC≌△DBC,∠A=110°,则∠D=110°. 如图,O是线段AB的中点,C在直线AB上,AC=4,CB=3,则OC的长等于0.5.
如图,O是线段AB的中点,C在直线AB上,AC=4,CB=3,则OC的长等于0.5.