题目内容
3.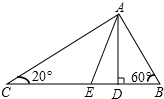 如图,在△ABC中,∠B=60°,∠C=20°,AD为△ABC的高,AE为角平分线.求∠EAD的度数.
如图,在△ABC中,∠B=60°,∠C=20°,AD为△ABC的高,AE为角平分线.求∠EAD的度数.
分析 首先根据三角形的内角和定理,求出∠BAC的度数是多少;然后根据AE为角平分线,求出∠BAE的度数是多少;最后在Rt△ABD中,求出∠BAD的度数,即可求出∠EAD的度数是多少.
解答 解:∵∠B=60°,∠C=20°,
∴∠BAC=180°-60°-20°=100°,
∵AE为角平分线,
∴∠BAE=100°÷2=50°,
∵AD为△ABC的高,
∴∠ADB=90°,
∴∠BAD=90°-60°=30°,
∴∠EAD=∠BAE-∠BAD=50°-30°=20°,
即∠EAD的度数是20°.
点评 (1)此题主要考查了三角形的内角和定理,要熟练掌握,解答此题的关键是要明确:三角形的内角和是180°.
(2)此题还考查了三角形的外角的性质和应用,要熟练掌握,解答此题的关键是要明确:①三角形的外角和为360°.②三角形的一个外角等于和它不相邻的两个内角的和.③三角形的一个外角大于和它不相邻的任何一个内角.

练习册系列答案
相关题目
14.下列式子中,表示y是x的正比例函数的是( )
| A. | y=$\frac{2}{x}$ | B. | y=x+2 | C. | y=x2 | D. | y=2x |
18.如图,一定数量的石子可以摆成如图所示的三角形和四边形,古希腊科学家把数1,3,6,10,15,21,…,称为“三角形数”;把1、4、9、16,25,…称为“正方形数”.同样的,可以把数1,5,12,22,…,等数称为“五边形数”.
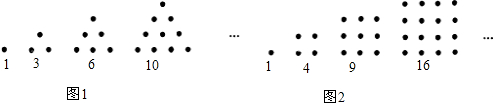
将三角形、正方形、五边形都整齐的由左到右填在所示表格里:
(1)按照规律,表格中a=28,b=36,c=35.
(2)观察表中规律,第n个“正方形数”是n2;若第n个“三角形数”是x,则用含x、n的代数式表示第n个“五边形数”是n2+x-n.
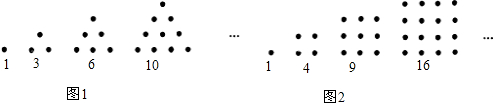
将三角形、正方形、五边形都整齐的由左到右填在所示表格里:
| 三角形数 | 1 | 3 | 6 | 10 | 15 | 21 | a | … |
| 正方形数 | 1 | 4 | 9 | 16 | 25 | b | 49 | … |
| 五边形数 | 1 | 5 | 12 | 22 | C | 51 | 70 | … |
(2)观察表中规律,第n个“正方形数”是n2;若第n个“三角形数”是x,则用含x、n的代数式表示第n个“五边形数”是n2+x-n.
8.已知平行四边形ABCD的对角线交于点O,则下列命题是假命题的是( )
| A. | 若AC⊥BD,则平行四边形ABCD是菱形 | |
| B. | 若BO=2AO,则平行四边形ABCD是菱形 | |
| C. | 若AB=AD,则平行四边形ABCD是菱形 | |
| D. | 若∠ABD=∠CBD,则平行四边形ABCD是菱形 |
13.以菱形ABCD的一个顶点A为圆心,以边AB长为半径画圆,被菱形截得的$\widehat{BD}$是40°,则菱形的一个钝角是( )
| A. | 140° | B. | 160° | C. | 100° | D. | 150° |
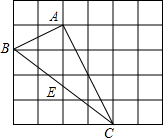 如图,在边长为1的小正方形组成的网格中,△ABC的三个顶点均在格点上,请按要求完成下列各题:
如图,在边长为1的小正方形组成的网格中,△ABC的三个顶点均在格点上,请按要求完成下列各题: