题目内容
14.在我国古代数学著作《九章算术》中记载了一道有趣的数学问题:“今有凫(凫:野鸭)起南海,七日至北海;雁起北海,九日至南海.今凫雁俱起,问何日相逢?”意思是:野鸭从南海起飞,7天飞到北海;大雁从北海起飞,9天飞到南海.野鸭与大雁从南海和北海同时起飞,经过几天相遇.设野鸭与大雁从南海和北海同时起飞,经过x天相遇,根据题意,下面所列方程正确的是( )| A. | (9-7)x=1 | B. | (9-7)x=1 | C. | ($\frac{1}{7}$+$\frac{1}{9}$)x=1 | D. | ($\frac{1}{7}$-$\frac{1}{9}$)x=1 |
分析 此题属于相遇问题,把南海到北海的距离看作单位“1”,野鸭的速度是$\frac{1}{7}$,大雁的速度为$\frac{1}{9}$,根据相遇时间=总路程÷速度和,即可列方程.
解答 解:设经过x天相遇,根据题意得:
($\frac{1}{7}$+$\frac{1}{9}$)x=1.
故选C.
点评 此题主要考查由实际问题抽象出一元一次方程,相遇问题中的基本数量关系:速度和×相遇时间=总路程,关键是由题目所给信息先分别求出二者的速度,速度=路程÷时间.

练习册系列答案
相关题目
2. 周末小石去博物馆参加综合实践活动,乘坐公共汽车0.5小时后想换乘另一辆公共汽车,他等候一段时间后改为利用手机扫码骑行摩拜单车前往.已知小石离家的路程s(单位:千米)与时间t(单位:小时)的函数关系的图象大致如图.则小石骑行摩拜单车的平均速度为( )
周末小石去博物馆参加综合实践活动,乘坐公共汽车0.5小时后想换乘另一辆公共汽车,他等候一段时间后改为利用手机扫码骑行摩拜单车前往.已知小石离家的路程s(单位:千米)与时间t(单位:小时)的函数关系的图象大致如图.则小石骑行摩拜单车的平均速度为( )
 周末小石去博物馆参加综合实践活动,乘坐公共汽车0.5小时后想换乘另一辆公共汽车,他等候一段时间后改为利用手机扫码骑行摩拜单车前往.已知小石离家的路程s(单位:千米)与时间t(单位:小时)的函数关系的图象大致如图.则小石骑行摩拜单车的平均速度为( )
周末小石去博物馆参加综合实践活动,乘坐公共汽车0.5小时后想换乘另一辆公共汽车,他等候一段时间后改为利用手机扫码骑行摩拜单车前往.已知小石离家的路程s(单位:千米)与时间t(单位:小时)的函数关系的图象大致如图.则小石骑行摩拜单车的平均速度为( )| A. | 30千米/小时 | B. | 18千米/小时 | C. | 15千米/小时 | D. | 9千米/小时 |
9.为解决“最后一公里”的交通接驳问题,平谷区投放了大量公租自行车供市民使用.据统计,目前我区共有公租自行车3 500辆.将3 500用科学记数法表示应为( )
| A. | 0.35×104 | B. | 3.5×103 | C. | 3.5×102 | D. | 35×102 |
19.一个猜想是否正确,科学家们要经过反复的论证.表是几位科学家“掷硬币”的实验数据:
请根据以上数据,估计硬币出现“正面朝上”的概率为0.50(精确到0.01).
| 实验者 | 德•摩根 | 蒲丰 | 费勒 | 皮尔逊 | 罗曼诺夫斯基 |
| 掷币次数 | 6 140 | 4 040 | 10 000 | 36 000 | 80 640 |
| 出现“正面朝上”的次数 | 3 109 | 2 048 | 4 979 | 18 031 | 39 699 |
| 频率 | 0.506 | 0.507 | 0.498 | 0.501 | 0.492 |
6.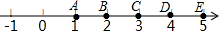 如图,在数轴上有A、B、C、D、E五个点表示相应的整数,无理数$\sqrt{13}$在两个点所表示的整数之间,这两个整数所对应的点是( )
如图,在数轴上有A、B、C、D、E五个点表示相应的整数,无理数$\sqrt{13}$在两个点所表示的整数之间,这两个整数所对应的点是( )
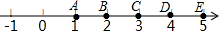 如图,在数轴上有A、B、C、D、E五个点表示相应的整数,无理数$\sqrt{13}$在两个点所表示的整数之间,这两个整数所对应的点是( )
如图,在数轴上有A、B、C、D、E五个点表示相应的整数,无理数$\sqrt{13}$在两个点所表示的整数之间,这两个整数所对应的点是( )| A. | 点A和点B | B. | 点B和点C | C. | 点C和点D | D. | 点D和点E |
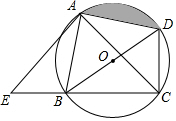 如图,四边形ABCD内接于⊙O,且BD为直径,∠ACB=45°,过A点的AC的垂线交BC的延长线于点E.
如图,四边形ABCD内接于⊙O,且BD为直径,∠ACB=45°,过A点的AC的垂线交BC的延长线于点E.
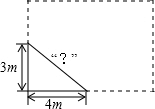 如图,学校有一块长方形花铺,有极少数人为了避开拐角走“捷径”,在花铺内走出了一条“路”.他们仅仅少走了( )步路(假设2步为1米),却踩伤了花草.
如图,学校有一块长方形花铺,有极少数人为了避开拐角走“捷径”,在花铺内走出了一条“路”.他们仅仅少走了( )步路(假设2步为1米),却踩伤了花草.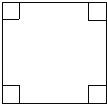 如图,面积为80cm2的大正方形的四个角是面积为5cm2的小正方形,现将这四个角剪掉,制作一个无盖的长方体盒子,求这个长方体的底面边长和高分别是多少?(结果保留根号)
如图,面积为80cm2的大正方形的四个角是面积为5cm2的小正方形,现将这四个角剪掉,制作一个无盖的长方体盒子,求这个长方体的底面边长和高分别是多少?(结果保留根号)