题目内容
6.关于x的方程|8x-1|+3x+||x+a|-3|-4=0有解,求a的取值范围.分析 题目含有一个单层绝对值和一个双重绝对值,首先利用求概率列举方式进行讨论,共分8种情况,然后利用绝对值性质去掉绝对值,求出未知数x的值,再将x的值代入相应取值范围,可以求a的取值范围.
解答 解:①当x<$\frac{1}{8}$,x+a<0,x+a+3<0时,
原式得:1-8x+3x+x+a+3-4=0,
解得:x=$\frac{a}{4}$,
代入①得:$\left\{\begin{array}{l}{\frac{a}{4}<\frac{1}{8}}\\{\frac{a}{4}+a<0}\\{\frac{a}{4}+a+3<0}\end{array}\right.$,
解得:a<-$\frac{12}{5}$.
②当x<$\frac{1}{8}$,x+a<0,x+a+3≥0时,
原式得:1-8x+3x-x-a-3-4=0,
解得:x=-1-$\frac{a}{6}$,
代入②得:$\left\{\begin{array}{l}{-1-\frac{a}{6}<\frac{1}{8}}\\{-1-\frac{a}{6}+a<0}\\{-1-\frac{a}{6}+a+3<0}\end{array}\right.$,
解得:-$\frac{27}{4}$<a$<-\frac{12}{5}$.
③当x<$\frac{1}{8}$,x+a≥0,x+a+3<0时,
原式得:1-8x+3x-x-a+3-4=0,
解得:x=-$\frac{a}{6}$
代入③得:$\left\{\begin{array}{l}{-\frac{a}{6}<\frac{1}{8}}\\{-\frac{a}{6}+a≥0}\\{-\frac{a}{6}+a+3<0}\end{array}\right.$,
解得:无解.
④当x<$\frac{1}{8}$,x+a≥0,x+a+3≥0时,
原式得:1-8x+3x+x+a-3-4=0,
解得:x=$\frac{a-6}{4}$,
代入④得:$\left\{\begin{array}{l}{\frac{a-6}{4}<\frac{1}{8}}\\{\frac{a-6}{4}+a≥0}\\{\frac{a-6}{4}+a+3≥0}\end{array}\right.$,
解得:$\frac{6}{5}$≤a<$\frac{13}{2}$.
⑤当x≥$\frac{1}{8}$,x+a<0,x+a+3<0时,
原式得:8x-1+3x+x+a+3-4=0,
解得:x=$\frac{2-a}{12}$,
代入⑤得:$\left\{\begin{array}{l}{\frac{2-a}{12}≥\frac{1}{8}}\\{\frac{2-a}{12}+a<0}\\{\frac{2-a}{12}+a+3<0}\end{array}\right.$,
解得:a<-$\frac{38}{11}$.
⑥当x≥$\frac{1}{8}$,x+a<0,x+a+3≥0时,
原式得:8x-1+3x-x-a-3-4=0,
解得:x=$\frac{a+8}{10}$,
代入⑥得:$\left\{\begin{array}{l}{\frac{a+8}{10}≥\frac{1}{8}}\\{\frac{a+8}{10}+a<0}\\{\frac{a+8}{10}+a+3≥0}\end{array}\right.$,
解得:-$\frac{38}{11}$≤a<-$\frac{8}{11}$.
⑦当x≥$\frac{1}{8}$,x+a≥0,x+a+3<0时,
原式得:8x-1+3x-x-a+3-4=0,
解得:x=$\frac{2+a}{10}$,
代入⑦得:$\left\{\begin{array}{l}{\frac{2+a}{10}≥\frac{1}{8}}\\{\frac{2+a}{10}+a≥0}\\{\frac{2+a}{10}+a+3<0}\end{array}\right.$,
解得:无解.
⑧当x≥$\frac{1}{8}$,x+a≥0,x+a+3≥0时,
原式得:8x-1+3x+x+a-3-4=0,
解得:x=$\frac{8-a}{12}$
代入⑧得:$\left\{\begin{array}{l}{\frac{8-a}{12}≥\frac{1}{8}}\\{\frac{8-a}{12}+a≥0}\\{\frac{8-a}{12}+a+3≥0}\end{array}\right.$
解得:-$\frac{8}{11}$≤a≤$\frac{13}{2}$.
综上所述:a的取值范围:a≤$\frac{13}{2}$.
点评 本题考查了含有绝对值符号的一元二次方程,题目的难点在于含有双重绝对值符号,对学生的思考问题又增加了难度.同时不等式组的运算也是本题考查的重点.

| A. | 2 | B. | 2或1 | C. | 1 | D. | 不能确定 |
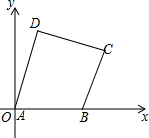 如图,在平面直角坐标系中,四边形各顶点的坐标分别为:A(0,0),B(7,0),C(9,5),D(2,7)
如图,在平面直角坐标系中,四边形各顶点的坐标分别为:A(0,0),B(7,0),C(9,5),D(2,7) 如图,已知∠BAC=∠DAC,请添加一个条件:AB=AD,使△ABC≌△ADC(写出一个即可).
如图,已知∠BAC=∠DAC,请添加一个条件:AB=AD,使△ABC≌△ADC(写出一个即可). 如图,两条公路0A和0B相交于点0,在∠A0B的内部有工厂C和D.现要修建一个货站P到两条公路0A、0B的距离相等,且到两工厂C、D的距离相等.用尺规作出货站P的位置.(要求:不写作法,保留作图痕迹,写出结论)
如图,两条公路0A和0B相交于点0,在∠A0B的内部有工厂C和D.现要修建一个货站P到两条公路0A、0B的距离相等,且到两工厂C、D的距离相等.用尺规作出货站P的位置.(要求:不写作法,保留作图痕迹,写出结论)