题目内容
4.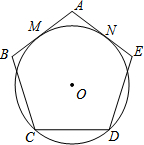 如图,半径为1的⊙O与正五边形ABCDE的边AB、AE相切于点M、N,则劣弧$\widehat{MN}$的长度为$\frac{2}{5}$π.
如图,半径为1的⊙O与正五边形ABCDE的边AB、AE相切于点M、N,则劣弧$\widehat{MN}$的长度为$\frac{2}{5}$π.
分析 连接OM,ON,首先根据切线的性质和正五边形的性质求得圆心角的度数,然后利用弧长公式进行计算.
解答 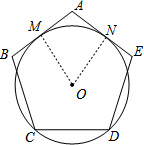 解:如图:连接OM,ON,
解:如图:连接OM,ON,
∵⊙O与正五边形ABCDE的边AB、AE相切于点M、N,
∴OM⊥AB,ON⊥AC,
∵∠A=108°,
∴∠MON=72°,
∵半径为1,
∴劣弧$\widehat{MN}$的长度为:$\frac{72π×1}{180}$=$\frac{2}{5}$π,
故答案为$\frac{2}{5}$π.
点评 本题考查了正多边形和圆的知识,解题的关键是能够连接OM和ON,从而求得劣弧所在扇形的圆心角,利用扇形弧长公式求解.

练习册系列答案
相关题目
19.在下列实数中,无理数是( )
| A. | sin45° | B. | $\frac{1}{3}$ | C. | 0.3 | D. | 3.14 |
16.某居民小区开展节约用电活动,该小区100户家庭4月份的节电情况如下表所示.
那么4月份这100户家庭的节电量(单位:千瓦时)的平均数是( )
| 节电量(千瓦时) | 20 | 30 | 40 | 50 |
| 户数(户) | 20 | 30 | 30 | 20 |
| A. | 35 | B. | 26 | C. | 25 | D. | 20 |
14.已知一等腰三角形的腰长为5,底边长为4,底角为α.满足下列条件的三角形与已知三角形不一定全等的是( )
| A. | 两个角是α,它们的夹边为4 | |
| B. | 三条边长分别是4,5,5 | |
| C. | 两条边长分别为4,5,它们的夹角为α | |
| D. | 两条边长是5,一个角是α |
