题目内容
14.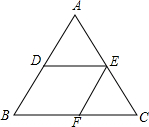 如图,DE∥BC,EF∥AC,则下列比例式中不正确的是( )
如图,DE∥BC,EF∥AC,则下列比例式中不正确的是( )| A. | $\frac{AE}{AC}=\frac{AD}{AB}$ | B. | $\frac{AE}{EC}=\frac{BF}{FC}$ | C. | $\frac{AD}{BD}=\frac{BF}{FC}$ | D. | $\frac{BD}{AD}=\frac{BF}{FC}$ |
分析 根据平行线分线段成比例定理逐个判断即可.
解答 解:A、∵DE∥BC,
∴$\frac{AE}{AC}$=$\frac{AD}{AB}$,故本选项错误;
B、∵EF∥AB,
∴$\frac{AE}{EC}$=$\frac{BF}{FC}$,故本选项错误;
C、∵DE∥BC,EF∥AC,
∴$\frac{AD}{BD}$=$\frac{AE}{EC}$,$\frac{AE}{EC}$=$\frac{BF}{FC}$,
∴$\frac{AD}{BD}$=$\frac{BF}{FC}$,故本选项错误;
D、∵$\frac{AD}{BD}$=$\frac{BF}{FC}$,故本选项正确;
故选D.
点评 本题考查了平行线分线段成比例定理的应用,能根据定理得出比例式是解此题的关键,注意:一组平行线截两条直线,所截得的线段对应成比例.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
3.若a、b互为相反数,则( )
| A. | ab>0 | B. | ab<0 | C. | ab≥0 | D. | ab≤0 |
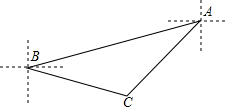 两艘巡逻艇同时从A港出发,如图所示,甲巡逻艇以$\frac{{16\sqrt{3}}}{5}$速度沿南偏西45°方向行进,乙巡逻艇以12km/h的速度沿南偏西75°方向行进4小时后,接到指挥中心指令,立即调整方向,沿南偏东75°方向以另一速度前进与直线行驶的甲巡逻艇在点C处相遇
两艘巡逻艇同时从A港出发,如图所示,甲巡逻艇以$\frac{{16\sqrt{3}}}{5}$速度沿南偏西45°方向行进,乙巡逻艇以12km/h的速度沿南偏西75°方向行进4小时后,接到指挥中心指令,立即调整方向,沿南偏东75°方向以另一速度前进与直线行驶的甲巡逻艇在点C处相遇 在直角坐标平面内,二次函数图象的顶点为A(1,-4),且过点B(3,0).
在直角坐标平面内,二次函数图象的顶点为A(1,-4),且过点B(3,0).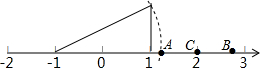 如图所示:数轴上点C所表示的数为2,点A与点B关于点C对称,则点B表示的数为5-$\sqrt{5}$.
如图所示:数轴上点C所表示的数为2,点A与点B关于点C对称,则点B表示的数为5-$\sqrt{5}$. 如图,把一张长方形的纸按图那样折叠后,B、D两点落在B′、D′点处,若得∠AOB′=80°,则∠B′OG的度数为50°.
如图,把一张长方形的纸按图那样折叠后,B、D两点落在B′、D′点处,若得∠AOB′=80°,则∠B′OG的度数为50°. 已知:点I是△ABC的内心,AI的延长线交外接圆于D.则DB与DI相等吗?为什么?
已知:点I是△ABC的内心,AI的延长线交外接圆于D.则DB与DI相等吗?为什么? 一架云梯长10m,如图所示斜靠在一面墙上,梯子底端C离墙6m.
一架云梯长10m,如图所示斜靠在一面墙上,梯子底端C离墙6m.