题目内容
16.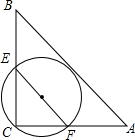 如图,Rt△ABC中,AC=4,AB=5,∠C=90°,经过点C且与边AB相切的圆与△ABC的边CB,CA分别相交于点E、F,线段EF长度的最小值为( )
如图,Rt△ABC中,AC=4,AB=5,∠C=90°,经过点C且与边AB相切的圆与△ABC的边CB,CA分别相交于点E、F,线段EF长度的最小值为( )| A. | 2.4 | B. | 2 | C. | 2.5 | D. | 2$\sqrt{2}$ |
分析 取EF的中点O,作OG⊥AB于G,CH⊥AB于H,连结OC,如图,先利用勾股定理计算出BC=3,再利用面积法计算出CH=2.4,接着根据圆周角定理可判断EF为经过点C且与边AB相切的圆的直径,点O为圆心,然后根据切线的性质得OG为⊙O的半径,则EF=OC+OG,利用垂线段最短,当OC、OG共线时,OC+OG的值最小,最小值为CH的长,于是得到EF的最小值为2.4.
解答 解:取EF的中点O,作OG⊥AB于G,CH⊥AB于H,连结OC,如图,
在Rt△ABC中,∵AC=4,AB=5,∠C=90°,
∴BC=$\sqrt{{5}^{2}-{4}^{2}}$=3,
∵$\frac{1}{2}$CH•AB=$\frac{1}{2}$BC•AC,
∴CH=$\frac{3×4}{5}$=2.4,
∵∠ECF=90°,
∴EF为经过点C且与边AB相切的圆的直径,点O为圆心,
∵AB为⊙O的切线,
∴OG为⊙O的半径,
∴EF=OC+OG,
当OC、OG共线时,OC+OG的值最小,最小值为CH的长,
∴EF的最小值为2.4.
故选A.
点评 本题考查了切线的性质:圆的切线垂直于经过切点的半径.运用切线的性质来进行计算或论证,常通过作辅助线连接圆心和切点,利用垂直构造直角三角形解决有关问题.

练习册系列答案
 能考试期末冲刺卷系列答案
能考试期末冲刺卷系列答案
相关题目
 ,则tanB的值为( )
,则tanB的值为( ) B.
B.  C.
C.  D.
D. 
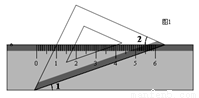
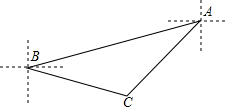 两艘巡逻艇同时从A港出发,如图所示,甲巡逻艇以$\frac{{16\sqrt{3}}}{5}$速度沿南偏西45°方向行进,乙巡逻艇以12km/h的速度沿南偏西75°方向行进4小时后,接到指挥中心指令,立即调整方向,沿南偏东75°方向以另一速度前进与直线行驶的甲巡逻艇在点C处相遇
两艘巡逻艇同时从A港出发,如图所示,甲巡逻艇以$\frac{{16\sqrt{3}}}{5}$速度沿南偏西45°方向行进,乙巡逻艇以12km/h的速度沿南偏西75°方向行进4小时后,接到指挥中心指令,立即调整方向,沿南偏东75°方向以另一速度前进与直线行驶的甲巡逻艇在点C处相遇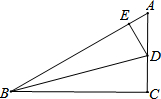 如图,在Rt△ABC中,∠C=90°,∠ABC=30°,BD是△ABC角平分线,求tan15°的值.(提示:过点D作DE⊥AB.垂足为点E.)
如图,在Rt△ABC中,∠C=90°,∠ABC=30°,BD是△ABC角平分线,求tan15°的值.(提示:过点D作DE⊥AB.垂足为点E.) 要求tan45°的值,可构造直角三角形进行计算,如图所示,作Rt△ABC,使∠C=90°,直角边AC=BC=1,斜边AB=$\sqrt{2}$.∠ABC=45°,所以tan45°=$\frac{AC}{BC}$=$\frac{1}{1}$=1.
要求tan45°的值,可构造直角三角形进行计算,如图所示,作Rt△ABC,使∠C=90°,直角边AC=BC=1,斜边AB=$\sqrt{2}$.∠ABC=45°,所以tan45°=$\frac{AC}{BC}$=$\frac{1}{1}$=1.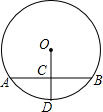 如图,已知⊙O的半径为5,弦AB的长为8,半径OD过AB的中点C,则CD的长为2.
如图,已知⊙O的半径为5,弦AB的长为8,半径OD过AB的中点C,则CD的长为2. 在直角坐标平面内,二次函数图象的顶点为A(1,-4),且过点B(3,0).
在直角坐标平面内,二次函数图象的顶点为A(1,-4),且过点B(3,0). 已知:点I是△ABC的内心,AI的延长线交外接圆于D.则DB与DI相等吗?为什么?
已知:点I是△ABC的内心,AI的延长线交外接圆于D.则DB与DI相等吗?为什么?