Question

如图，正方形ABCD内部有若干个点，用这些点以及正方形ABCD的顶点A、B、C、D把原正方形分割成一些三角形（互相不重叠）：

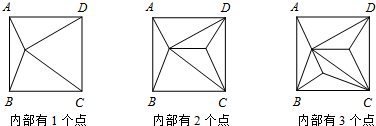
（1）填写下表

正方形ABCD内点的个数	1	2	3	4	…	n
分割成的三角形的个数m	4	6

（2）原正方形能否被分割成2014个三角形？若能，求此时正方形ABCD内部有多少个点？若不能，请说明理由．

Answer 1

考点：规律型：图形的变化类

专题：

分析：（1）由图形中三角形的个数，并观察发现，每多一个点，三角形的个数增加2，然后据此规律填表即可；
（2）根据（1）中规律，列式求解，如果n是整数，则能分割，如果不是整数，则不能分割．

解答：解：（1）有1个点时，内部分割成4个三角形；
有2个点时，内部分割成4+2=6个三角形；
有3个点时，内部分割成4+2×2=8个三角形；
有4个点时，内部分割成4+2×3=10个三角形；
…
以此类推，有n个点时，内部分割成4+2×（n-1）=（2n+2）个三角形；
填写下表

正方形ABCD内点的个数	1	2	3	4	…	n
分割成的三角形的个数m	4	6	8	10		2n+2

（2）能．
理由如下：由（1）知2n+2=2014，
解得n=1006，
∴此时正方形ABCD内部有1006个点．

点评：此题考查图形的变化规律，根据数据的变化规律，结合图形，总结出每增加一个点，三角形的个数增加2的规律是解题的关键．