题目内容
19. 如图,已知等边△ABC以边BC为直径的半圆与边AB、AC分别交于点D、点E,过点E作EF⊥AB,垂足为点F.
如图,已知等边△ABC以边BC为直径的半圆与边AB、AC分别交于点D、点E,过点E作EF⊥AB,垂足为点F.(1)请判断EF与⊙O的位置关系,并证明你的结论;
(2)过点F作FH⊥BC,垂足为点H,若等边△ABC的边长为8,求FH的长.(结果保留根号)
分析 (1)首先得出△OCE是等边三角形,进而利用平行线的判定与性质得出EF⊥EO,即可得出答案;
(2)直接利用三角形中位线的性质得出AE的长,再利用直角三角形的性质得出答案.
解答 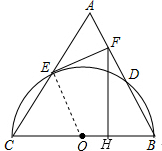 解:(1)EF是⊙O的切线,
解:(1)EF是⊙O的切线,
理由:连接EO,
∵△ABC是等边三角形,
∴∠B=∠C=∠A=60°,
∵EO=CO,
∴△OCE是等边三角形,
∴∠EOC=∠B=60°,
∴EO∥AB,
∵EF⊥AB,
∴EF⊥EO,
∴EF是⊙O的切线;
(2)∵EO∥AB,
∴EO是△ACB的中位线,
∵AC=8,
∴AE=CE=4,
∵∠A=60°,EF⊥AB,
∴∠AEF=30°,
∴AF=2,
∴BF=6,
∵FH⊥BC,∠B=60°.
∴∠BFH=30°,
∴BH=3,
∴FH2=BF2-BH2,
∴FH=3$\sqrt{3}$.
点评 此题主要考查了直线和圆的位置以及三角形中位线定理等知识,正确得出△OCE是等边三角形是解题关键.

练习册系列答案
相关题目
7. 将正整数按如图所示的规律排列下去,现有等式An=(i,j)表示正整数n是第i排第j个数(从左往右数),如A9=(4,3),则A113等于( )
将正整数按如图所示的规律排列下去,现有等式An=(i,j)表示正整数n是第i排第j个数(从左往右数),如A9=(4,3),则A113等于( )
 将正整数按如图所示的规律排列下去,现有等式An=(i,j)表示正整数n是第i排第j个数(从左往右数),如A9=(4,3),则A113等于( )
将正整数按如图所示的规律排列下去,现有等式An=(i,j)表示正整数n是第i排第j个数(从左往右数),如A9=(4,3),则A113等于( )| A. | (15,8) | B. | (15,9) | C. | (16,8) | D. | (16,9) |
4.下列实数中最小的数是( )
| A. | π | B. | -$\sqrt{10}$ | C. | 12 | D. | -3 |
11.在下列实数$\frac{22}{7}$,2.14139265,$\sqrt{8}$,-8,$\root{3}{9}$,$\sqrt{36}$,$\frac{π}{3}$中无理数有( )
| A. | 3个 | B. | 4个 | C. | 5个 | D. | 6个 |
9.下列定理中没有逆定理的是( )
| A. | 直角三角形的两个锐角互余 | B. | 等腰三角形两腰上的高相等 | ||
| C. | 全等三角形周长相等 | D. | 两直线平行,内错角相等 |
 如图,矩形纸片ABCD中,AB=8,AD=6,折叠纸片使点A落在对角线BD上的点F处,折痕为DE,则AE的长为3.
如图,矩形纸片ABCD中,AB=8,AD=6,折叠纸片使点A落在对角线BD上的点F处,折痕为DE,则AE的长为3.