题目内容
【题目】阅读理解
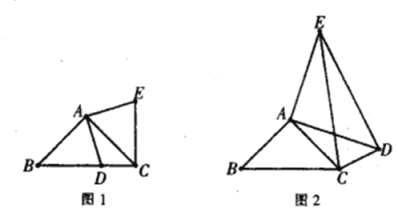
如图1，
中，沿
的平分线
折叠，剪掉重叠部分；将余下部分沿
的平分线
折叠，剪掉重叠部分；……；将余下部分沿
的平分线
折叠，点
与点
重合，无论折叠多少次，只要最后一次恰好重合，我们就称是的好角．
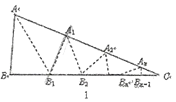
情形一：如图2，沿等腰三角形
顶角的平分线折叠，点
与点重合；
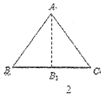
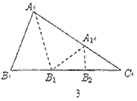
情形二：如图3，沿的的平分线折叠，剪掉重叠部分；将余下的部分沿的平分线折叠，此时点
与点重合．
探究发现
（1）中，
，经过两次折叠，问 的好角（填写“是”或“不是”）；
（2）若经过三次折叠发现是的好角，请探究
与
（假设
）之间的等量关系 ；
根据以上内容猜想：若经过
次折叠
是的好角，则与（假设）之间的等量关系为 ；
应用提升：
（3）小丽找到一个三角形，三个角分别为
，
，
，发现 是此三角形的好角；
（4）如果一个三角形的最小角是
，且满足该三角形的三个角均是此三角形的好角；
则此三角形另外两个角的度数 ．
【答案】（1）是；（2）
；
；（3）
和
；（4）另外两个角的度数分别为
和
【解析】
（1）由沿
的平分线
折叠，得
，且
，沿
的平分线
折叠，此时点
与
重合，可得
，即可证
.
（2）由沿的平分线折叠，得，由将余下部分沿的平分线折叠，得
，最后沿
的平分线
折叠,点
与点重合，得
，由
，可证；由小丽展示的情形一当
时；由探究（1）当时；由探究（2）当时，它们的均是
的好角；可推经过
次折叠，是的好角，则
与
的等量关系为.
（3）由（2）得，可计算
是的好角.
（4）由（2）知，是的好角，已知中一个三角形的最小角是，且这个三角形三个角均是的好角，可设另外两个角为
、
，（其中
都是正整数），依题意列式
，可求解得.
（1）中，，经过两次折叠，是的好角；
理由如下：
沿的平分线折叠，
；
将余下部分沿的平分线折叠，此时点与重合，
；
；
，
故答案是：是；
（2）在中,沿的平分线折叠,剪掉重复部分;将余下部分沿的平分线折叠,剪掉重复部分,将余下部分沿的平分线折叠,点与点重合,则是的好角.
证明：
，
，
，
，
，
，
由小丽展示的情形一知，当时，是的好角；
由探究（1）知，当时，是的好角；
由探究（2）知，当时，是的好角；
故若经过次折叠，是的好角，则与的等量关系为.
故答案为：
.
（3）由（2）知，，
，
，
是的好角.
故答案为：.
（4）由（2）知，是的好角，一个三角形的最小角是，且这个三角形三个角均是的好角，可设另外两个角为、，（其中都是正整数）.
依题意得，
化简得
，
都是正整数，
都是17的整数因子，
，
，
，
，
，
，
即该三角形的另外两个角是：和.
故答案为：
.
