题目内容
【题目】如图,△ABC中,∠ACB=90°,AB=5cm,BC=3cm,若点P从点A出发,以每秒2cm的速度沿折线A﹣C﹣B﹣A运动,设运动时间为t秒(t>0).
(1)若点P在AC上,且满足PA=PB时,求出此时t的值;
(2)若点P恰好在∠BAC的角平分线上,求t的值;
(3)在运动过程中,直接写出当t为何值时,△BCP为等腰三角形.
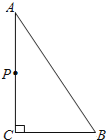
【答案】(1) ![]() ;(2)
;(2)![]() 或6;(3)当
或6;(3)当![]() 或
或![]() 时,△BCP为等腰三角形.
时,△BCP为等腰三角形.
【解析】
(1)设存在点P,使得![]() ,此时
,此时![]() ,
,![]() ,根据勾股定理列方程即可得到结论;
,根据勾股定理列方程即可得到结论;
(2)当点P在![]() 的平分线上时,如图1,过点P作
的平分线上时,如图1,过点P作![]() 于点E,此时
于点E,此时![]() ,
,![]() ,
,![]() ,根据勾股定理列方程即可得到结论;
,根据勾股定理列方程即可得到结论;
(3)在![]() 中,根据勾股定理得到
中,根据勾股定理得到![]() ,根据题意得:
,根据题意得:![]() ,当P在AC上时,
,当P在AC上时,![]() 为等腰三角形,得到
为等腰三角形,得到![]() ,即
,即![]() ,求得
,求得![]() ,当P在AB上时,
,当P在AB上时,![]() 为等腰三角形,若
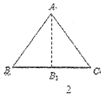
为等腰三角形,若![]() ,点P在BC的垂直平分线上,如图2,过P作
,点P在BC的垂直平分线上,如图2,过P作![]() 于E,求得
于E,求得![]() ,若
,若![]() ,即
,即![]() ,解得
,解得![]() ,
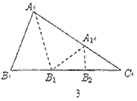
,![]() ,如图3,过C作
,如图3,过C作![]() 于F,由射影定理得;
于F,由射影定理得;![]() ,列方程
,列方程![]() ,即可得到结论.
,即可得到结论.
解:在![]() 中,
中,![]() ,
,![]() ,
,
![]() ,
,
(1)设存在点P,使得![]() ,
,
此时![]() ,
,![]() ,
,
在![]() 中,
中,![]() ,
,
即:![]() ,
,
解得:![]() ,
,
![]() 当
当![]() 时,
时,![]() ;
;
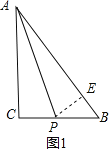
(2)当点P在![]() 的平分线上时,如图1,过点P作
的平分线上时,如图1,过点P作![]() 于点E,
于点E,
此时![]() ,
,![]() ,
,![]() ,
,
在![]() 中,
中,![]() ,
,
即:![]() ,
,
解得:![]() ,
,
当![]() 时,点
时,点![]() 与
与![]() 重合,也符合条件,
重合,也符合条件,
![]() 当
当![]() 或6时,
或6时,![]() 在
在![]() 的角平分线上;
的角平分线上;
(3)根据题意得:![]() ,
,
当P在AC上时,![]() 为等腰三角形,
为等腰三角形,
![]() ,即
,即![]() ,
,
![]() ,
,
当P在AB上时,![]() 为等腰三角形,
为等腰三角形,
![]() ,点P在BC的垂直平分线上,
,点P在BC的垂直平分线上,
如图2,过P作![]() 于E,
于E,

![]() ,
,
![]() ,即
,即![]() ,解得:
,解得:![]() ,
,
![]() ,即
,即![]() ,
,
解得:![]() ,
,
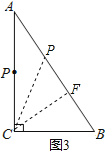
![]() ,如图3,过C作
,如图3,过C作![]() 于F,
于F,
![]() ,
,
![]() ,
,
由射影定理得;![]() ,
,
即![]() ,
,
解得:![]() ,
,
![]() 当
当![]() 时,
时,![]() 为等腰三角形.
为等腰三角形.

练习册系列答案
相关题目