题目内容
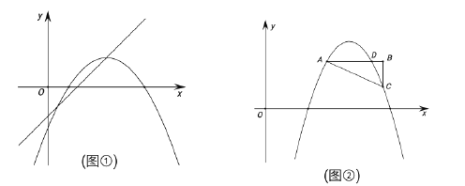
【题目】如图1 ,在![]() 中,
中,![]()
![]() 是
是![]() 边上一点(不与点
边上一点(不与点![]() 重合),将线段
重合),将线段![]() 绕点
绕点![]() 逆时针旋转
逆时针旋转![]() 得到
得到![]() ,连接
,连接![]() .
.
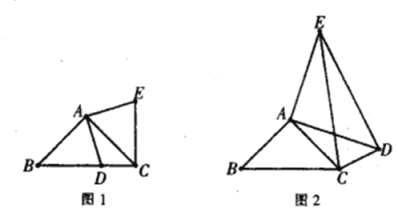
(发现问题)
(1)如图1 ,通过图形旋转的性质,可知![]() _______,
_______,![]() 度;
度;
(解决问题)
(2)如图1,证明![]() ;
;
(拓展延伸)
如图2,在![]() 中,
中,![]() 为
为![]() 外一点,且
外一点,且![]() ,仍将线段
,仍将线段![]() 绕点
绕点![]() 逆时针旋转
逆时针旋转![]() 得到
得到![]() ,连接
,连接![]() .
.
(3)若![]() 求的
求的![]() 长.
长.
【答案】(1)AE;90;(2)见解析;(3)BD的长为9
【解析】
![]() 利用旋转变换的性质即可解决问题;
利用旋转变换的性质即可解决问题;
![]() 证明
证明![]() ≌
≌![]() ,推出
,推出![]() ,等量代换即可得结论;
,等量代换即可得结论;
![]() 如图2中,连接
如图2中,连接![]() ,证明
,证明![]() ≌
≌![]() ,推出
,推出![]() ,再证明
,再证明![]() 是直角三角形,利用两次勾股定理即可解决问题.
是直角三角形,利用两次勾股定理即可解决问题.
解:(1)由旋转性质:对应点到旋转中心的距离相等;对应点与旋转中心所连线段的夹角等于旋转角,得到![]() .
.
故答案为:AE;90.
(2)∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
又∵![]() ,
,
∴![]() (SAS),
(SAS),
∴![]() ,
,
∴![]() ;
;
(3)如图2中,连BD.

∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
又![]() ,
,![]() ,
,![]() ≌
≌![]() ,
,![]() ,
,
∵![]() ,
,![]() ,
,
∴![]() ,
,![]() ,
,![]() 为直角三角形,
为直角三角形,![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() .
.

练习册系列答案
 出彩同步大试卷系列答案
出彩同步大试卷系列答案
相关题目