Question

如图，矩形ABCD，AB=2，BC=4，F为线段BC上的一动点，且不和B、C重合，连接FA，过点F作FE⊥FA交CD所在直线于E，将△FEC沿FE翻折到△FEG位置，使点G落到AD上，则BF=

 

．

Answer 1

考点：翻折变换（折叠问题）

专题：综合题

分析：作FH⊥AD于H，如图，设BF=x，则CF=4-x，利用等角的余角相等得到∠1=∠3，则根据相似三角形的判定得到Rt△ABF∽Rt△FCE，利用相似比得CE=

x(4-x)

2

，再根据折叠的性质得EG=CE=

x(4-x)

2

，FG=FC=4-x，∠FGE=∠C=90°，所以DE=DC-CE=2-

x(4-x)

2

，∠5+∠6=90°，然后证明Rt△FHG∽Rt△GDE，利用相似比得到GD=x，在Rt△DGE中，根据勾股定理得[2-

x(4-x)

2

]²+x²=[

x(4-x)

2

]²，整理得3x²-8x+4=0，最后解一元二次方程即可．

解答：解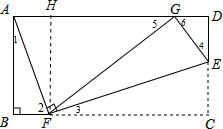：作FH⊥AD于H，如图，设BF=x，则CF=4-x，
∵FE⊥FA，
∴∠2+∠3=90°，
而∠1+∠2=90°，
∴∠1=∠3，
∴Rt△ABF∽Rt△FCE，
∴

AB

FC

=

BF

CE

，即

2

4-x

=

x

CE

，
∴CE=

x(4-x)

2

，
∵△FEC沿FE翻折到△FEG位置，使点G落到AD上，
∴EG=CE=

x(4-x)

2

，FG=FC=4-x，∠FGE=∠C=90°，
∴DE=DC-CE=2-

x(4-x)

2

，∠5+∠6=90°，
而∠4+∠6=90°，
∴∠5=∠4，
∴Rt△FHG∽Rt△GDE，
∴

FH

GD

=

FG

GE

，即

2

GD

=

4-x

x(4-x) 2

，
∴GD=x，
在Rt△DGE中，
∵DE²+DG²=GE²，
∴[2-

x(4-x)

2

]²+x²=[

x(4-x)

2

]²，
整理得3x²-8x+4=0，解得x₁=

2

3

，x₂=2，
即BF的长为

2

3

或2．
故答案为

2

3

或2．

点评：本题考查了折叠的性质：折叠是一种对称变换，它属于轴对称，折叠前后图形的形状和大小不变，位置变化，对应边和对应角相等．也考查了矩形的性质和相似三角形的判定与性质．