题目内容
8.函数y=$\sqrt{\frac{x-3}{x-2}}$的自变量的取值范围是x≥3或x<2.分析 根据二次根式的性质和分式的意义,被开方数大于或等于0,分母不等于0,可以求出x的范围.
解答 解:y=$\sqrt{\frac{x-3}{x-2}}$的自变量的取值范围$\left\{\begin{array}{l}{x-3≥0}\\{x-2>0}\end{array}\right.$,或$\left\{\begin{array}{l}{x-3≤0}\\{x-2<0}\end{array}\right.$,
解得x≥3或x<2,
故答案为:x≥3或x<2.
点评 本题考查了函数自变量的取值范围,函数自变量的范围一般从三个方面考虑:当函数表达式是整式时,自变量可取全体实数;当函数表达式是分式时,考虑分式的分母不能为0;当函数表达式是二次根式时,被开方数非负.

练习册系列答案
 明天教育课时特训系列答案
明天教育课时特训系列答案 浙江新课程三维目标测评课时特训系列答案
浙江新课程三维目标测评课时特训系列答案 周周清检测系列答案
周周清检测系列答案 轻巧夺冠周测月考直通高考系列答案
轻巧夺冠周测月考直通高考系列答案
相关题目
3.下列计算正确的是( )
| A. | a2×a3=a6 | B. | (a+b)2=a2+b2 | C. | (a+b)(a-b)=a2-b2 | D. | (a2)3=a5 |
17.在函数y=$\sqrt{1-2x}$中,自变量x的取值范围是( )
| A. | x<$\frac{1}{2}$ | B. | x≤$\frac{1}{2}$ | C. | x>$\frac{1}{2}$ | D. | x≥$\frac{1}{2}$ |
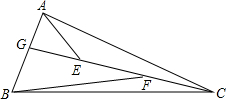 已知△AEG、△AEC、△BFG、△BCF的面积分别为2,5,7,3平方厘米,则△EFB的面积为$\frac{29}{7}$平方厘米.
已知△AEG、△AEC、△BFG、△BCF的面积分别为2,5,7,3平方厘米,则△EFB的面积为$\frac{29}{7}$平方厘米.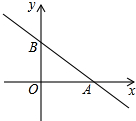 如图,一次函数y=kx+b的图象交y轴于点B(0,3),与x轴正半轴交于点A,cos∠BAO=$\frac{4}{5}$
如图,一次函数y=kx+b的图象交y轴于点B(0,3),与x轴正半轴交于点A,cos∠BAO=$\frac{4}{5}$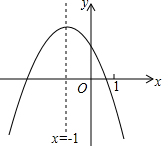 二次函数y=ax2+bx+c(a≠0)的图象如图,给出下列四个结论:
二次函数y=ax2+bx+c(a≠0)的图象如图,给出下列四个结论: