题目内容
已知：Rt△ABC中，∠C=90°，AB=15，AC=9，则斜边AB上的高CD的长为 ．
考点：勾股定理,三角形的面积
专题：
分析：先用勾股定理求出直角边BC的长度，再用面积就可以求出斜边上的高．
解答：解：在Rt△ABC中
由勾股定理得：BC=
=12，
由面积公式得：S△ABC=
AC•BC=
AB•CD
∴CD=
=
=7.2．
故斜边AB上的高CD的长为7.2．
故答案为：7.2．
由勾股定理得：BC=
| AB2-AC2 |
由面积公式得：S△ABC=
| 1 |
| 2 |
| 1 |
| 2 |
∴CD=
| AC×BC |
| AB |
| 12×9 |
| 15 |
故斜边AB上的高CD的长为7.2．
故答案为：7.2．
点评：考查了勾股定理，利用勾股定理和直角三角形的面积相结合，求解斜边上的高是解直角三角形的重要题型之一，也是中考的热点．
练习册系列答案
双基同步导航训练系列答案
黄冈小状元同步计算天天练系列答案
相关题目
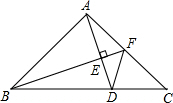已知△ABC，AB=AC，∠BAC=90°，点F在AC上，BF⊥AD垂足为E．若DE=2，∠AFB=∠CFD，则△ADF的面积为
如图，在△ABC中，CD⊥AE，∠BAE=25°，∠BCD=20°，则∠B=