题目内容
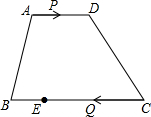 如图,在梯形ABCD中,AD∥BC,AD=8,BC=15,点E在BC边上,且CE=2BE.点P以每秒1个单位长度的速度从点A出发,沿AD向点D运动;点Q同时以每秒3个单位长度的速度从点C出发,沿CB向点B运动,当其中一个点停止运动时,另一个点也随之停止运动.当运动时间t=
如图,在梯形ABCD中,AD∥BC,AD=8,BC=15,点E在BC边上,且CE=2BE.点P以每秒1个单位长度的速度从点A出发,沿AD向点D运动;点Q同时以每秒3个单位长度的速度从点C出发,沿CB向点B运动,当其中一个点停止运动时,另一个点也随之停止运动.当运动时间t=考点:平行四边形的判定,梯形
专题:动点型
分析:由已知以点P,Q,E,D为顶点的四边形是平行四边形有两种情况:(1)当Q运动到E和B之间;(2)当Q运动到E和C之间;根据平行四边形的判定,由AD∥BC,所以当PD=QE时为平行四边形.根据此设运动时间为t,列出关于t的方程求解.
解答: 解:由已知梯形,
解:由已知梯形,
(1)当Q运动到E和B之间,设运动时间为t,
∵AD=8,BC=15,CE=2BE,
∴EC=10,
则得:QE=PD,
3t-10=8-t,
解得:t=
,
(2)当Q运动到E和C之间,设运动时间为t,则得:DP′=EQ′,
10-3t=8-t,
解得:t=1,
故答案为:1或
.
 解:由已知梯形,
解:由已知梯形,(1)当Q运动到E和B之间,设运动时间为t,
∵AD=8,BC=15,CE=2BE,
∴EC=10,
则得:QE=PD,
3t-10=8-t,
解得:t=
| 9 |
| 2 |
(2)当Q运动到E和C之间,设运动时间为t,则得:DP′=EQ′,
10-3t=8-t,
解得:t=1,
故答案为:1或
| 9 |
| 2 |
点评:此题考查的知识点是梯形及平行四边形的性质,关键是由已知明确有两种情况,不能漏解.

练习册系列答案
 智能训练练测考系列答案
智能训练练测考系列答案 计算高手系列答案
计算高手系列答案
相关题目
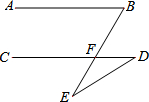 如图,已知AB∥CD,∠B=60°,∠D=32°,求∠E.
如图,已知AB∥CD,∠B=60°,∠D=32°,求∠E. (1)请把图中的四边形ABCD先向左平移6个单位,再向下平移8个单位,画出平移后的四边形,并指出四边形ABCD中各顶点的坐标;
(1)请把图中的四边形ABCD先向左平移6个单位,再向下平移8个单位,画出平移后的四边形,并指出四边形ABCD中各顶点的坐标; 如图,E、F是平行四边形ABCD的对角线AC上的点,CE=AF.求证:四边形BEDF是平行四边形.
如图,E、F是平行四边形ABCD的对角线AC上的点,CE=AF.求证:四边形BEDF是平行四边形. 如图,△ABC中,D、E分别是AB、AC上的点(DE不平行于BC),要使△CDE与△ABC相似,则图中应补充的一个条件是
如图,△ABC中,D、E分别是AB、AC上的点(DE不平行于BC),要使△CDE与△ABC相似,则图中应补充的一个条件是 如图,圆柱体的高为8cm,底面周长为4cm,小蚂蚁在圆柱表面爬行,从A点到B点,路线如图,则最短路程为
如图,圆柱体的高为8cm,底面周长为4cm,小蚂蚁在圆柱表面爬行,从A点到B点,路线如图,则最短路程为