题目内容
如图，E、F是平行四边形ABCD的对角线AC上的点，CE=AF．求证：四边形BEDF是平行四边形．考点：平行四边形的判定与性质
专题：证明题
分析：由CE=AF，可得AE=CF，连接BD交AC于O，则可知OB=OD，OA=OC，又AE=CF，所以OE=OF，然后依据对角线互相平分的四边形是平行四边形即可证明．
解答：证明：∵CE=AF，
∴CE-EF=AF-EF
即AE=CF，
如图：
连接BD交AC于O，
∵四边形ABCD是平行四边形，
∴AO=CO，BO=DO
∵AE=CF，
∴AO-AE=CO-CF．
即EO=FO．
∴四边形BEDF为平行四边形（对角线互相平分的四边形是平行四边形）．
∴CE-EF=AF-EF
即AE=CF，
如图：
连接BD交AC于O，
∵四边形ABCD是平行四边形，
∴AO=CO，BO=DO
∵AE=CF，
∴AO-AE=CO-CF．
即EO=FO．
∴四边形BEDF为平行四边形（对角线互相平分的四边形是平行四边形）．
点评：此题主要考查了平行四边形的判定，掌握平行四边形的判定方法是解决问题的关键．
练习册系列答案
相关题目
如图，在平面直角坐标系中，
在数轴上近似地表示下列各数，并把这些数按从小到大顺序进行排列，用“＜”连接．4，-1.5，0，-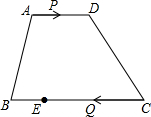
如图，在梯形ABCD中，AD∥BC，AD=8，BC=15，点E在BC边上，且CE=2BE．点P以每秒1个单位长度的速度从点A出发，沿AD向点D运动；点Q同时以每秒3个单位长度的速度从点C出发，沿CB向点B运动，当其中一个点停止运动时，另一个点也随之停止运动．当运动时间t=