题目内容
如图，△ABC中，D、E分别是AB、AC上的点（DE不平行于BC），要使△CDE与△ABC相似，则图中应补充的一个条件是考点：相似三角形的判定
专题：
分析：根据相似三角形判定定理：两个角相等的三角形相似；夹角相等，对应边成比例的两个三角形相似，即可解题．
解答：解：∵∠C是公共角，
如果∠CDE=∠B或∠CED=∠A，
∴△ADE∽△ABC；
如果
=
，∠C=∠C，
∴△ADE∽△ABC，
故答案为：∠CDE=∠B或∠CED=∠A或
=
．
如果∠CDE=∠B或∠CED=∠A，
∴△ADE∽△ABC；
如果
| CE |
| AC |
| CD |
| BC |
∴△ADE∽△ABC，
故答案为：∠CDE=∠B或∠CED=∠A或
| CE |
| AC |
| CD |
| BC |
点评：此题主要考查学生对相似三角形判定的理解和掌握，此题答案不唯一，具有较强的开放性．
练习册系列答案
一线名师提优试卷系列答案
相关题目
在数轴上近似地表示下列各数，并把这些数按从小到大顺序进行排列，用“＜”连接．4，-1.5，0，-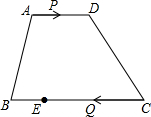
如图，在梯形ABCD中，AD∥BC，AD=8，BC=15，点E在BC边上，且CE=2BE．点P以每秒1个单位长度的速度从点A出发，沿AD向点D运动；点Q同时以每秒3个单位长度的速度从点C出发，沿CB向点B运动，当其中一个点停止运动时，另一个点也随之停止运动．当运动时间t=
如图，长方形内有两个相邻的正方形，面积分别为4和3，那么阴影部分的面积为