题目内容
如图，圆柱体的高为8cm，底面周长为4cm，小蚂蚁在圆柱表面爬行，从A点到B点，路线如图，则最短路程为考点：平面展开-最短路径问题
专题：
分析：沿过A点和过B点的母线剪开，展成平面，连接AB则AB的长是蚂蚁在圆柱表面从A点爬到B点的最短路程，求出AC和BC的长，根据勾股定理求出斜边AB即可．
解答：
解：沿过A点和过B点的母线剪开，展成平面，连接AB．则AB的长是蚂蚁在圆柱表面从A点爬到B点的最短路程，
AC=
×4=6，∠C=90°，BC=8，
由勾股定理得：AB=
=10，
故答案为：10．
解：沿过A点和过B点的母线剪开，展成平面，连接AB．则AB的长是蚂蚁在圆柱表面从A点爬到B点的最短路程，AC=
| 3 |
| 2 |
由勾股定理得：AB=
| 62+82 |
故答案为：10．
点评：本题考查了平面展开-最短路线问题和勾股定理的应用，关键是知道求出AB的长就是蚂蚁在圆柱表面从A点爬到B点的最短路程．
练习册系列答案
相关题目
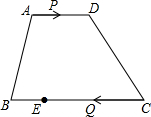如图，在梯形ABCD中，AD∥BC，AD=8，BC=15，点E在BC边上，且CE=2BE．点P以每秒1个单位长度的速度从点A出发，沿AD向点D运动；点Q同时以每秒3个单位长度的速度从点C出发，沿CB向点B运动，当其中一个点停止运动时，另一个点也随之停止运动．当运动时间t=
如图，长方形内有两个相邻的正方形，面积分别为4和3，那么阴影部分的面积为