题目内容
7．把下列多项式因式分解：（1）x2-4y2+x+2y；
（2）（x+y）2-4（x+y-1）；
（3）xn+1-2xn+xn-1（n是大于1的正整数）．
分析 （1）把前两项分为一组，运用平方差公式，后两项分为一组，再提公因式即可；
（2）变形为（x+y）2-4（x+y）+4，再运用完全平方公式进行因式分解即可；
（3）先提公因式xn-1，再运用完全平方公式因式分解即可．
解答 解：（1）原式=（x2-4y2）+（x+2y）
=（x+2y）（x-2y）+（x+2y）
=（x+2y）（x-2y-1）；
（2）原式=（x+y）2-4（x+y）+4，
=（x+y+2）2；
（3）原式=xn-1（x2-2x+1），
=xn-1（x-1）2．
点评 本题考查了因式分解中的分组分解，掌握分组的方法以及平方差公式和完全平方公式是解题的关键．
练习册系列答案
相关题目
17．
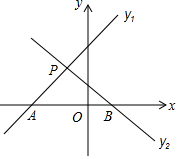如图，已知直线y1=k1x+m和直线y2=k2x+n交于点P（-1，2），则关于x的不等式（k1-k2）x＞-m+n的解是（ ）
如图，已知直线y1=k1x+m和直线y2=k2x+n交于点P（-1，2），则关于x的不等式（k1-k2）x＞-m+n的解是（ ）| A． | x＞2 | B． | x＞-1 | C． | -1＜x＜2 | D． | x＜-1 |
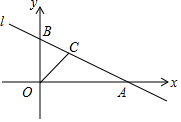如图，直线l：y=-0.5x+2与x轴、y轴相交于点A，B．OC是∠ABO的角平分线．
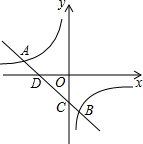如图，一次函数y=kx+b的图象与反比例函数y=$\frac{m}{x}$的图象交于A（-3，1），B（2，n）两点，直线AB分别交x轴、y轴于D，C两点．
如图，AD是△ABC的角平分线，DF⊥AB，垂足为F，DE=DG，△ADG和△AED的面积分别是30，18，则△DEF的面积为6．
如图，正方形ABCD的边长为1，点P为BC上任意一点（可以与B点或C重合），分别过B，C，D作射线AP的垂线，垂足分别是B'，C'，D'，则BB'+CC'+DD'的最大值与最小值的和为2+$\sqrt{2}$．
5．下列对分式-$\frac{1}{1-x}$的变形，正确的是（ ）
| A． | $\frac{1}{x-1}$ | B． | $-\frac{1}{x-1}$ | C． | $-\frac{1}{1+x}$ | D． | $\frac{1}{1+x}$ |
